Типовые воздействия

Процессы в системе автоматического управления возникают под влиянием внешних воздействий на систему. Внешними воздействиями могут быть управляющие воздействия, или возмущения. В реальных условиях внешние воздействия могут иметь произвольный характер и выражаться произвольными функциями времени как детерминированными, так и статистическими. Поскольку в этом случае задача исследования становится неопределенной, то при анализе систем автоматического управления используют ряд типовых воздействий, которые позволяют наиболее полно выявить динамические свойства исследуемой системы и в то же время наиболее близки к реальным внешним воздействиям.

В теории автоматического управления используются следующие типовые воздействия при изучении переходных процессов в системе.

1. Ступенчатая функция (скачкообразное воздействие).

График ступенчатой функции приведен на рис. 31. В нулевой момент времени воздействие скачком изменяется от нуля до некоторой постоянной величины. Аналитическое выражение для ступенчатой функции

.

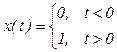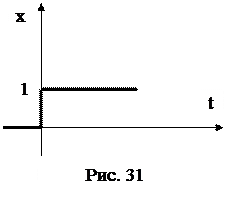При значении функции, равном единице (рис. 31), функция называется единичной ступенчатой функцией. Единичную функцию обозначают

x(t) = 1(t) = [1].

Если амплитуда ступенчатой функции отличается от единицы и равна некоторой величине А, то такая функция является неединичной и обозначается

x(t) = A[1].

Изображения Лапласа для ступенчатой функци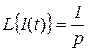и

и .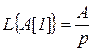

2. Единичная импульсная функция, или дельта-функция.

Эта функция представляет собой производную от единичной ступенчатой функции .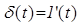

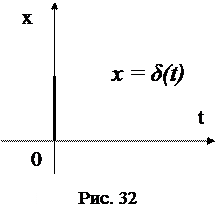Дельта-функция равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности (рис. 32).

Основное свойство дельта-функции

,

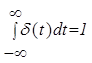т.е. она имеет единичную площадь.

Размерность единичной 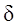-функции [сек^–1]. 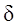-функцию можно рассматривать как предел прямоугольного импульса при стремлении его длительности к нулю, а амплитуды - к бесконечности. С помощью импульсной функции удобно моделировать ударные воздействия на систему (кратковременные воздействия – удары).

3. Гармоническая функция.

Функция, изменяющаяся по гармоническому закону (закону синуса или косинуса) (рис. 33):

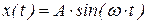или .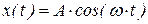

В теории автоматического управления гармоническую функцию часто записывают с использованием формулы Эйлера

.

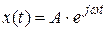Гармоническая функция применяется при исследовании частотных свойств элементов и систем автоматического управления. С её помощью моделируются повторяющиеся периодические воздействия (например, вибрации).

4. Степенные функции времени.

Выражают линейное, квадратичное и т.д. изменение входной величины во времени:

,

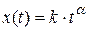где k – постоянный коэффициент, a - константа.

При a=1 обеспечивается линейная функция времени, график которой приведен на рис. 34.

Степенные функции применяются в том случае, когда необходимо смоделировать непрерывное изменение воздействия на систему, например, при исследовании следящих систем.

---

Дата добавления: 2015-09-02