N – кратному дифференцированию оригинала соответствует умножение изображения на pn.

3. Интегрирование оригинала

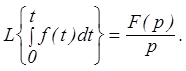
Интегрированию интеграла в пределах от 0 до t соответствует деление изображения на р.

4. Смещение аргумента оригинала

, при этом , если .

Смещению аргумента оригинала на соответствует умножение изображения на .

5. Смещение аргумента изображения

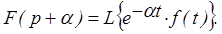
Смещению аргумента изображения на 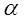соответствует умножение оригинала .

6. Умножение изображений (теория свертывания)

Операция 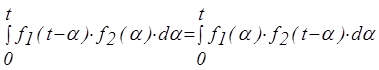называется сверткой.

Изображение свертки двух оригиналов равно произведению их изображений.

Переход от изображения к оригиналу осуществляется с помощью обратного преобразования Лапласа, выполняемого с использованием формулы обращения:

где С – абсцисса абсолютной сходимости, выбирается так, чтобы все полюсы подынтегральной функции находились слева от нее (рис. 28). Всегда должно быть С > s₀. На рис. 28 ´ – полюсы функции-изображения.

Обозначение обратного преобразования Лапласа осуществляется символом L^-1 или 1/L.

.

Непосредственное использование формулы обращения вызывает значительные сложности. Для упрощения обратного перехода используются таблицы, приводимые в справочниках, и специальные приемы.

Так, если функция-изображение является дробной функцией: , то при выполнении обратного преобразования Лапласа применимо разложение Хевисайда. Пусть функция имеет m полюсов (корней уравнения B(p)=0), тогда

Пример. Выше мы получили для постоянной величины

Осуществим обратное преобразование Лапласа, используя разложение Хевисайда. В этом случае A(p)=A, B(p)=p, p_k=0, m=1,

, следовательно,

В результате обратного преобразования с использованием разложения Хевисайда получена постоянная величина А, что и следовало ожидать.

Дата добавления: 2015-09-02