Понятие обыкновенной линейной системы

Система автоматического управления называется обыкновенной линейной, если процесс в системе можно описать обыкновенным линейным дифференциальным уравнением порядка " n ". Это уравнение записывается в следующем виде:

где у(t) – выходная (управляемая) величина, х(t) – входное воздействие, c_i, b_j – постоянные коэффициенты уравнения, n > m.

Реальные САУ и их элементы обычно имеют нелинейные статические характеристики и описываются нелинейными дифференциальными уравнениями. Однако на практике в ряде случаев нелинейностью можно пренебречь и описать САУ или ее элемент линеаризованным (приведённым к линейному виду) дифференциальным уравнением.

Таким образом, обыкновенная линейная система является упрощенной математической моделью для описания реальных систем автоматического управления. Процессы в обыкновенной линейной системе описываются обыкновенными линейными дифференциальными уравнениями любого порядка "n". Все сигналы в такой системе непрерывны и связаны между собой линейными функциональными зависимостями.

Обыкновенное линейное дифференциальное уравнение порядка "n" в теории автоматического управления принято записывать в операторном виде

,

где 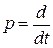- оператор дифференцирования.

Решение дифференциального уравнения y(t) дает описание процесса в системе, возникающего при воздействии на ее вход сигнала x(t). Решение дифференциального уравнения складывается из общего решения и частного решения:

,

где - общее решение дифференциального уравнения без правой части, описывающее свободный процесс в системе независимо от вида входного воздействия; - частное решение дифференциального уравнения, зависящее от его правой части и описывающее вынужденный процесс в системе.

Для нахождения общего решения нужно решить уравнение без правой части

.

Общее решение обыкновенного линейного дифференциального уравнения порядка "n" имеет вид

,

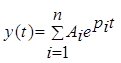где A_i – постоянные интегрирования, определяемые из начальных условий ; p_i – корни характеристического уравнения

.

В статическом состоянии системы все сигналы в ней постоянны и, следовательно, все производные этих сигналов равны нулю. Тогда

и дифференциальное уравнение системы вырождается в статическую характеристику

или ,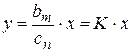

где K – коэффициент усиления системы.

Теория обыкновенных линейных систем автоматического управления была разработана в первую очередь и является базой для теории автоматического управления.

Дата добавления: 2015-09-02