Преобразование Лапласа

В теории автоматического управления широко используются методы операционного исчисления. Суть операционного исчисления заключается в том, что каждой рассматриваемой функции f(t), называемой оригиналом, ставится в соответствие по определенным законам некоторая другая функция F(p), называемая изображением. При этом математические операции над оригиналами заменяются математическими операциями над изображениями.

Законы соответствия между оригиналами и изображениями выбраны таким образом, чтобы математические операции над оригиналами заменялись бы более простыми математическими операциями над изображениями. При использовании преобразования Лапласа операции дифференцирования и интегрирования оригиналов сводятся к операциям умножения и деления изображений на независимую переменную.

В результате применения преобразования Лапласа к обыкновенному линейному дифференциальному уравнению ему в области изображений будет соответствовать линейное алгебраическое уравнение. Решение уравнения для изображений будет существенно проще, что упрощает исследование системы автоматического регулирования.

В преобразовании Лапласа устанавливается интегральная связь между изображением и оригиналом:

где - произвольная комплексная величина, являющаяся аргументом для изображающей функции.

Оригиналом f(t) может быть функция действительного переменного, если она обладает следующими свойствами:

1) f(t) определена и дифференцируема на всей числовой прямой;

2) f(t)=0 при t<0;

3) существуют такие положительные величины M>0 и S₀, что

при .

Для линейных обыкновенных дифференциальных уравнений, описывающих процессы в системах автоматического управления, перечисленные требования выполняются.

В преобразовании Лапласа оригинал обозначается строчной буквой, а изображение - соответствующей ей прописной буквой. Применяется одно из следующих обозначений преобразования Лапласа:

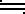
, или .

Пример. Найдем изображения Лапласа для некоторых функций. Пусть f(t)=A=const, тогда

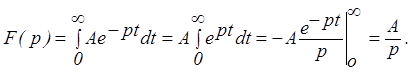
Другая функция f(t)=t

Аналогично вычисляются изображения других функций. Для наиболее распространенных функций их лапласовы изображения приводятся в справочных пособиях по математике и теории автоматического управления.

Дата добавления: 2015-09-02