Передаточная функция. Обыкновенная линейная система автоматического управления описывается обыкновенным

Обыкновенная линейная система автоматического управления описывается обыкновенным линейным дифференциальным уравнением

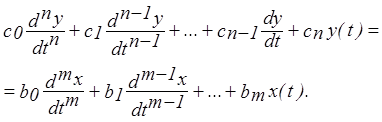
Умножим обе части уравнения на е ^{– pt} и выполним интегрирование в пределах от 0 до :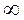

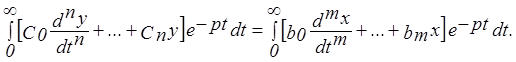
В результате этих преобразований левая и правая части уравнения представляют собой выражения для преобразования Лапласа. Осуществим преобразование Лапласа, используя его свойства:

.

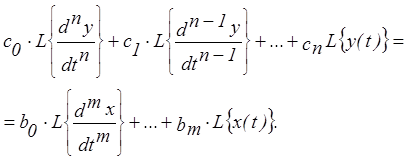Полагая, что система находится при нулевых начальных условиях
y (0) = 0, y '(0) = y '' (0) =... = 0, вычислим изображения производных и получим

.

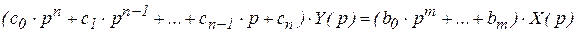Полученное уравнение является алгебраическим уравнением и его можно решить относительно изображения выходной величины:

.

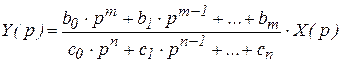Передаточной функцией элемента (или системы) автоматического управления называется отношение Лапласовых изображений выходной и входной величин

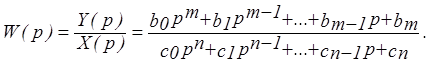
При нахождении передаточной функции подразумевается, что элемент (или система) находится при нулевых начальных условиях.

Передаточная функция является дробно-рациональной функцией от независимой переменной р. Передаточная функция легко получается из исходного дифференциального уравнения формальной подстановкой вместо производных символа р в соответствующей степени.

При р = 0 передаточная функция вырождается в коэффициент передачи. Обычно для передаточной функции m < n.

При известной передаточной функции процесс в системе определяется следующим образом:

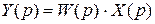и .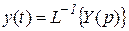

Корни числителя передаточной функции называются нулями передаточной функции, корни знаменателя передаточной функции – полюсами. В общем случае передаточная функция имеет m нулей и n полюсов. Нули и полюса могут быть комплексными.

Дата добавления: 2015-09-02