Временные характеристики системы автоматического управления

Временная характеристика представляет собой переходный процесс на выходе системы автоматического управления, возникающий при подаче на вход системы внешнего воздействия. Различают два вида временных характеристик.

Первая временная характеристика получила название переходной характеристики и представляет собой процесс в системе при воздействии на вход системы ступенчатой функции. Изображение Лапласа для переходной характеристики (переходного процесса)

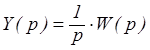или .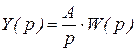

Переходная характеристика является функцией времени и определяется только динамическими свойствами системы:

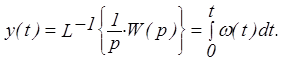
В обыкновенных линейных системах можно наблюдать три основных вида переходных характеристик (рис. 35).

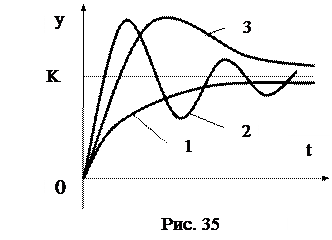
1. Апериодические (монотонные). Первая производная выходной величины не меняет знака.

2. Колебательные периодические. Первая производная выходной величины меняет знак бесконечное число раз.

3. Апериодические колебательные. Первая производная выходной величины меняет свой знак, но отсутствует периодичность смены знака производной и число экстремумов ограничено.

Вид переходной характеристики определяется динамическими свойствами системы или ее элемента. Поэтому при анализе системы автоматического управления обычно стремятся определить её переходную характеристику для оценки свойств системы.

Вторая временная характеристика описывает реакцию (отклик) системы на входное воздействие, описываемое единичной импульсной дельта-функцией. Воздействие дельта-функции выводит систему из состояния равновесия, и дальнейшее поведение системы определяется её собственными свойствами, поскольку внешнее воздействие прекращается (d(t) ≡ 0 при t > 0). Эта временная характеристика получила название функции веса.

Изображение Лапласа единичной импульсной функции X(p) = L{d (t)} = 1, тогда изображение для функции веса

.

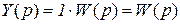Сама весовая функция (функция времени) определится как

.

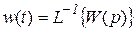Весовая функция описывает процесс в системе, возникающий при подаче на вход системы сигнала в виде единичной импульсной функции, и выражается оригиналом передаточной функции системы. Таким образом, вид весовой функции полностью определяется свойствами системы.

Поскольку изображение Лапласа для процесса в системе

,

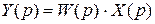то сам процесс в системе можно выразить через весовую функцию системы, используя свойство умножения изображений для преобразования Лапласа:

.

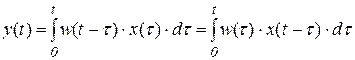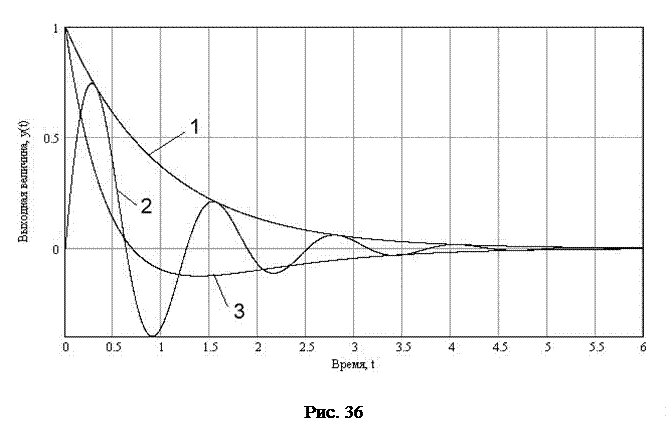
Полученная формула позволяет непосредственно описывать переходный процесс в системе при любом входном воздействии по известной функции веса системы. Поскольку весовая функция однозначно определяется передаточной функцией системы, то и характер процесса, описываемого весовой функцией, для обыкновенной линейной системы будет соответствовать переходной характеристике системы. На рис. 36 приведены типовые графики для весовой функции обыкновенной линейной системы автоматического управления. График 1 соответствует апериодическому процессу, график 2 – колебательному, график
3 – колебательному апериодическому.

Дата добавления: 2015-09-02