Автоматического управления. Частотные характеристики системы автоматического управления определяются при

Частотные характеристики системы автоматического управления определяются при подаче на вход системы гармонического воздействия

,

где 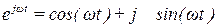(формула Эйлера).

При подаче такого сигнала на вход и после затухания переходных процессов на выходе установятся также гармонические колебания с той же частотой w, но с другой амплитудой и фазой (рис. 37). Тогда для выходного сигнала можно записать

y(t) = y_m = y_m ,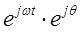

где - угол фазового сдвига выходного сигнала относительно входного; - период сигнала; w - круговая частота сигнала.

Пусть исследуемая линейная система описывается обыкновенным линейным дифференциальным уравнением

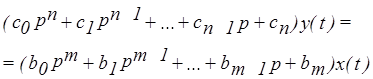
При гармоническом входном сигнале можно в этом уравнении определить все производные входной величины

,

,

....................................................................................

.

Аналогично определятся и производные выходной величины. В результате исходное дифференциальное уравнение можно переписать в виде алгебраического уравнения

Решив это уравнение, получим

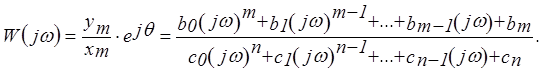
Величина W(j ) называется комплексной частотной функцией (или частотной передаточной функцией). Комплексная частотная функция может быть найдена по передаточной функции путем подстановки p = jw:

Частотная передаточная функция может быть записана в комплексном виде

где А(w) – модуль частотной передаточной функции; (w) – фазовый угол (аргумент); U(w) = Re W(jw) – вещественная составляющая передаточной функции; V(w) = Jm W(jw) – мнимая составляющая частотной передаточной функции.

Для частотной передаточной функции справедливы следующие соотношения:

, .

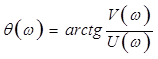Зависимости А() и q() определяют изменение амплитуды и фазы колебаний на выходе системы при изменении частоты входных колебаний. Модуль частотной характеристики A(w) определяет коэффициент усиления системы для гармонического сигнала с частотой w.

Дата добавления: 2015-09-02