Построение частотных характеристик системы

Структура обыкновенной линейной системы автоматического управления всегда будет состоять из типовых звеньев, рассмотренных выше. Эти звенья будут входить в структуру в составе различных соединений: последовательного, параллельного, соединения с обратной связью.

Передаточная функция системы, состоящей из различных соединений типовых звеньев, выразится зависимостью вида

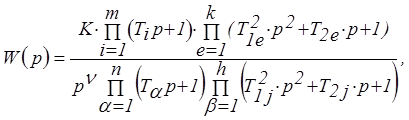
где K – коэффициент усиления системы.

Сомножители вида , стоящие в знаменателе выражения, соответствуют инерционным звеньям, входящим в последовательные соединения. Сомножители в знаменателе соответствуют колебательным звеньям, соединённым последовательно. Предполагается, что в системе n инерционных звеньев и h колебательных звеньев.

Параметр p в знаменателе передаточной функции появляется при наличии в структуре системы интегрирующих звеньев. Таких звеньев может быть в системе ν, поскольку при наличии в системе интегрирующего звена система становится астатической, то число интегрирующих звеньев ν называют степенью астатизма системы.

Структура системы может содержать параллельные соединения звеньев. Пусть, например, в системе присутствует параллельное соединение усилительного и интегрирующего звена, тогда передаточная функция этого соединения

.

Из-за присутствия в системе параллельного соединения типовых звеньев в числителе передаточной функции появляются сомножители вида 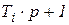. Для обозначения таких сомножителей их условно приписывают форсирующим звеньям первого порядка. Форсирующее звено первого порядка имеет динамические свойства, обратные свойствам инерционного звена. Аналогично, сомножители вида приписывают форсирующим звеньям второго порядка, свойства которых противоположны свойствам колебательного звена.

Таким образом, передаточная функция обыкновенной линейной системы будет состоять из произведений типовых сомножителей. Поскольку каждый сомножитель соответствует структурному звену с типовыми динамическими свойствами, то и динамические свойства системы в целом будут комбинацией типовых свойств. Это обстоятельство, в частности, позволяет упростить построение частотных характеристик линейной системы.

Сделав подстановку в приведенное выше выражение для передаточной функции системы, можно перейти к частотной передаточной функции

модуль которой

Используя последнее выражение для амплитудной логарифмической частотной характеристики системы, можно записать

В соответствии с последним выражением для нахождения суммарной амплитудной логарифмической характеристики системы необходимо построить ЛАХ для входящих в систему звеньев, а затем геометрически их суммировать.

Исходя из общего выражения для частотной передаточной функции, можно записать выражение для фазового угла системы

Сомножители числителя частотной передаточной функции обеспечивают положительные фазовые сдвиги, а сомножители знаменателя – отрицательные. Фазовая частотная характеристика системы получается суммированием фазовых частотных характеристик составляющих систему типовых звеньев.

Асимптотическая ЛАХ строится ещё проще, и ее построение рассмотрим на примере. Пусть передаточная функция системы имеет вид

тогда частотная передаточная функция запишется в виде

а модуль частотной передаточной функции

Логарифмическая амплитудная характеристика

при этом слагаемое будет влиять на ход характеристики при , слагаемое 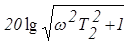- при и т.д.

Частоты называются частотами сопряжения. Учет влияния каждого следующего звена при построении асимптотической характеристики ведется для частот, более высоких, чем соответствующая частота сопряжения, путем изменения наклона характеристики на 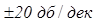, в зависимости от знака, стоящего перед слагаемым (на -20 дБ/дек для инерционного звена и +20 дБ/дек для форсирующего звена первого порядка).

В результате суммарная асимптотическая логарифмическая амплитудная характеристика для рассматриваемого примера примет вид, изображенной на рис. 72, где для определенности принято .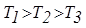

Если одно из звеньев системы колебательное, то на соответствующей ему частоте сопряжения наклон характеристики изменяется на 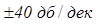(-40 дБ/дек для колебательного звена и +40 дБ/дек для форсирующего звена второго порядка).

Общие правила построения асимптотической ЛАХ линейной системы следующие:

· асимптотическая ЛАХ состоит из прямолинейных отрезков, имеющих разный наклон к оси частот, кратный 20 дБ/дек;

· низкочастотный участок ЛАХ проходит через точку 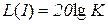и имеет наклон 0 дБ/дек для статической системы и дБ/дек для астатической системы с астатизмом ν порядка;

· влияние каждого звена на ЛАХ системы учитывается начиная с частоты сопряжения, определяемой постоянной времени звена;

· учет влияния звена сводится к изменению наклона очередного отрезка ЛАХ на частоте сопряжения следующим образом:

* наклон увеличивается на –20 дБ/дек для инерционного звена,

* наклон уменьшается на +20 дБ/дек для форсирующего звена первого порядка,

* наклон увеличивается на –40 дБ/дек для колебательного звена,

* наклон уменьшается на +40 дБ/дек для форсирующего звена второго порядка.

Суммарная логарифмическая фазовая характеристика получается суммированием фазовых характеристик звеньев системы. Для рассмотренного примера фазовая частотная логарифмическая характеристика показана на рис. 73: 1 – ЛФХ интегрирующего звена, 2 – ЛФХ форсирующего звена первого порядка, 3 и 4 – ЛФХ инерционных звеньев, 5 – суммарная фазовая частотная характеристика.

Суммарная фазовая характеристика 5 получена суммированием ординат (с учетом знака) фазовых характеристик звеньев. На рис. 73 положительная полуось фазовых углов направлена вниз.

При построении частотных характеристик системы замена действительной ЛАХ асимптотической ЛАХ для колебательного звена даёт значительную погрешность при малой степени успокоения звена. Если для колебательного звена степень успокоения выходит за пределы 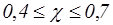, то асимптотическая ЛАХ нуждается в уточнении. Для этого строится точная характеристика путем расчета точек по формулам для колебательного звена (в пределах дек от частоты сопряжения). Учесть особенности характеристики можно также, используя график поправок для ЛАХ колебательного звена, который приводится в литературе по теории управления.

Дата добавления: 2015-09-02