Дифференцирующее звено.

Дифференцирующее звено реализует функцию дифференцирования входного сигнала. Для этого звена выходной сигнал пропорционален скорости изменения входного сигнала. Уравнение дифференцирующего звена

,
переходная характеристика для дифференцирующего звена представляет собой усиленную в k раз импульсную дельта-функцию (рис. 53).

Уравнение звена в операторном виде

,
откуда передаточная функция звена

.

Частотная функция дифференцирующего звена

,
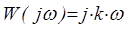при этом , Модуль частотной характеристики растёт с ростом частоты и стремится к бесконечности. Фазовый угол от частоты не зависит и постоянно равен 90°. Эти особенности отражает АФЧХ дифференцирующего звена, показанная на рис. 54. АФЧХ располагается вдоль положительной полуоси мнимых чисел на комплексной плоскости. Начало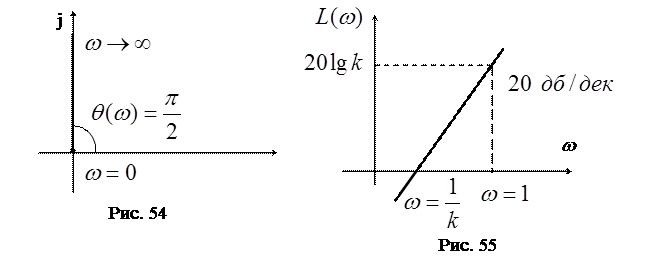
АФЧХ, соответствующее частоте , совпадает с началом координат, а при 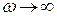АФЧХ устремляется в бесконечность.

Выражения для логарифмических частотных характеристик получаем на основе выражения частотной передаточной функции

,

.

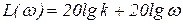Выражение для ЛАХ описывает прямую линию с наклоном +20 дБ/дек, проходящую через точку с координатами , , а ЛФХ изобразится горизонтальной прямой на уровне 90°.Общий вид логарифмических частотных характеристик дифференцирующего звена приведен на рис. 55.

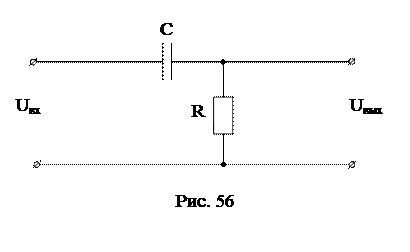Описанное дифференцирующее звено обладает идеальными свойствами и рассматривается как идеальное дифференцирующее звено. Реально осуществить дифференцирующее звено с идеальными свойствами невозможно. Схема реального дифференцирующего звена показана на рис. 56, это хорошо известная дифференцирующая RC-цепь.

Реальное дифференцирующее звено описывается уравнением

.
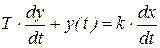Переходная характеристика реального дифференцирующего звена

,
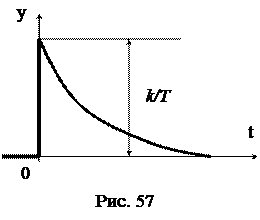
её вид показан на рис. 57. Переходная характеристика реального дифференцирующего звена существенно отличается от переходной характеристики идеального дифференцирующего звена. Поэтому реальное дифференцирующее звено выполняет операцию дифференцирования сигнала с погрешностью. Эта погрешность зависит от постоянной времени T: чем больше постоянная времени, тем при прочих равных условиях погрешность больше.

Передаточная функция реального дифференцирующего звена

а его частотная передаточная функция

Модуль и аргумент частотной характеристики:

, .

Амплитудно-фазовая частотная характеристика реального дифференцирующего звена показана на рис. 58, а его асимптотическая логарифмическая амплитудная характеристика - на рис. 59.

Дата добавления: 2015-09-02