Применение критерия к логарифмическим характеристикам

При использовании критерия Найквиста можно рассматривать не амплитудно-фазовую частотную характеристику системы, а ее логарифмические частотные характеристики. Пусть разомкнутая система устойчива, тогда устойчивость замкнутой системы по Найквисту определится положением годографа W(jw) по отношению к контрольной точке (рис. 86).

Если годограф W(jw) не охватывает контрольную точку (кривая 1), то замкнутая система устойчива, если охватывает (кривая 2), – система неустойчива. В точке пересечения АФЧХ с отрицательным направлением вещественной оси (частота w₁) угол фазового сдвига . Для устойчивой системы частота среза w_с (при этой частоте АФЧХ пересекает единичную окружность и при этом , а ) меньше частоты w₁, при которой фазовый угол равен -p. Для неустойчивой системы соотношение этих частот обратное: .

Таким образом, для устойчивой системы частота среза меньше частоты для фазового угла в -p, а для неустойчивой системы соотношение этих частот обратное. Это условие легко проверяется с использованием логарифмических частотных характеристик системы.

На рис. 87 показаны логарифмические частотные характеристики для устойчивой (1) и неустойчивой (2) систем: L(w) – логарифмическая амплитудная характеристика (ЛАХ), q(w) – логарифмическая фазовая характеристика (ЛФХ), w _с – частота среза системы, w ₁ – частота фазового угла -p (или -180°).

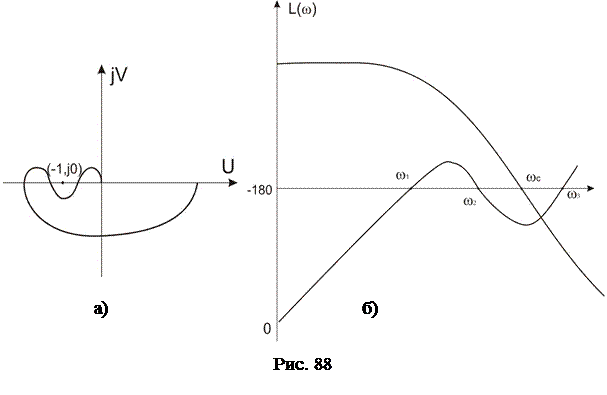
Для устойчивой системы 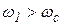и частота , при которой угол фазового сдвига , соответствует области отрицательных ординат логарифмической амплитудной характеристики L(w). Для неустойчивой системы (логарифмическая амплитудная характеристика 2) и частота w₁ соответствует области положительных значений ординат ЛАХ (т.е. на этой частоте коэффициент усиления системы больше единицы).

Следовательно, система будет устойчива, если точка пересечения ЛАХ с осью частот лежит левее точки пересечения ЛФХ с прямой, соответствующей фазовому сдвигу .

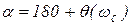Для устойчивой системы величина угла (рис. 87) характеризует запас устойчивости системы по фазе, ордината ЛАХ - запас устойчивости системы по амплитуде.

В том случае, когда АФЧХ системы имеет вид ("клювообразный" вид), показанный на рис. 88а, ЛФХ будет пересекать границу несколько раз (рис. 88б). В этом случае для устойчивости системы необходимо, чтобы число пересечений ЛФХ границы , лежащих левее частоты среза ,было бы четным. На рис. 88б левее частоты среза имеются два пересечения на частотах w₁ и w₂, следовательно, система устойчива.

Логарифмический критерий устойчивости обладает большой простотой и наглядностью, что обуславливает его распространенность при исследовании устойчивости системы. Если использовать асимптотические логарифмические частотные характеристики системы, то простота применения критерия ещё более очевидна.

---

Дата добавления: 2015-09-02