Критерий устойчивости Гурвица

Критерий Гурвица использует для оценки выполнения условия устойчивости системы коэффициенты характеристического уравнения замкнутой системы. Следовательно, для применения критерия Гурвица необходим характеристический полином замкнутой системы

.

Первым условием устойчивости системы автоматического управления по Гурвицу является положительность всех коэффициентов c_i характеристического уравнения. Если это условие не соблюдается, то система неустойчива. Для заключения об устойчивости системы условия положительности коэффициентов недостаточно.

Вторым условием устойчивости системы по Гурвицу является положительность всех определителей, составленных из коэффициентов характеристического полинома на основе таблицы Гурвица. Для уравнения n-порядка таблица Гурвица имеет следующий вид:

C1	C3	C5	C7	C9
C0	C2	C4	C6	C8
	C1	C3	C5	C7
	C0	C2	C4	C6
		C1	C3	C5
	…	…	…	…	….
	…	…	…	…	….	Cn
					….	Cn-1
					….	Cn-2	Cn

При составлении таблицы по ее главной диагонали выписываются все коэффициенты характеристического уравнения, начиная с c₁ по c_n. Затем каждый столбец таблицы, начиная с главной диагонали, дополняется коэффициентами: вверх - с возрастающим номером, вниз - с убывающим номером. Вместо отсутствующих коэффициентов ставятся нули. В результате получается таблица (матрица), содержащая нули и коэффициенты характеристического полинома замкнутой системы.

На основе таблицы составляются определители

; …

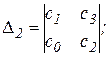
Критерий Гурвица сводится к требованию положительности всех n определителей, составленных на основе таблицы, т.е. должно быть

, , … .

Условием нахождения системы на границе устойчивости является равенство нулю последнего определителя

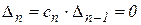или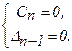

определяет границу устойчивости апериодического типа, 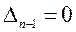- границу устойчивости колебательного типа.

Например, для системы третьего порядка характеристический полином

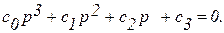
Таблица Гурвица для этого случая будет иметь следующий вид:

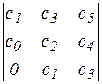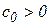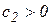Для устойчивости системы необходимо выполнение требований ; ; ; , а также

При исследовании устойчивости по Гурвицу достаточно рассмотреть знак главных определителей, которые определяют знак всех остальных (зависимых) определителей. В литературе по теории управления на основе раскрытия определителей приводятся конечные условия устойчивости для систем разного порядка.

Используя критерий Гурвица, можно исследовать влияние того или иного параметра на устойчивость системы и определить допустимые границы изменения этого параметра. При исследовании находят зависимость для определителей от влияющего параметра x: 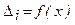, и затем строят графики функций этих зависимостей (рис. 80).

По графикам можно видеть, что условие устойчивости соблюдается только при изменении влияющего параметра x в пределах от Х_{mi n} до Х_max, поскольку только в этих границах все определители остаются положительными одновременно. Следовательно, по графику необходимо определить область изменения влияющего параметра, в которой все определители положительны одновременно. Изменение влияющего параметра в установленных таким образом пределах не приводит к потере системой устойчивости. Подобное исследование может потребоваться при необходимости ответа на вопрос о возможности замены того или иного элемента системы (например, при ремонте) без потери системой работоспособности.

Алгебраический критерий Гурвица удобно применять для исследования замкнутых систем автоматического регулирования, для которых известна передаточная функция замкнутой системы и, следовательно, известен характеристический полином замкнутой системы. При практическом применении критерия нет необходимости каждый раз составлять таблицу Гурвица и определители на её основе. Достаточно вычислить главные определители, выражения для которых применительно к системам разного порядка приводятся в учебной и справочной литературе по теории автоматического управления.

Дата добавления: 2015-09-02