Критерий устойчивости Найквиста

Критерий Найквиста является частотным критерием и дает возможность судить об устойчивости замкнутой системы по виду амплитудно-фазовой частотной характеристики разомкнутой системы. Частотная передаточная функция разомкнутой системы может быть получена из передаточной функции разомкнутой системы

Амплитудно-фазовая частотная характеристика системы представляет собой годограф вектора на комплексной плоскости при изменении частоты в пределах . Об устойчивости замкнутой системы судят по виду этого годографа.

Рассмотрим основы критерия Найквиста. Пусть разомкнутая система устойчива и её передаточная функция

,

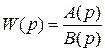где B(p) - характеристический полином разомкнутой системы. Так как система устойчива, то характеристический полином не имеет правых корней.

Для замкнутой системы передаточная функция

.

Частотная характеристика замкнутой системы

.

Представим

,

где 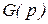- характеристический полином замкнутой системы, - характеристический полином разомкнутой системы. Степень этих полиномов одинакова и равна n – порядку системы.

Комплексы и можно представить векторами на комплексной плоскости. Если изменять частоту 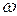в пределах 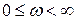, то вектор повернется вокруг начала координат на угол , так как система устойчива и характеристический полином разомкнутой системы не содержит правых корней.

Поворот вектора будет зависеть от устойчивости замкнутой системы. Если замкнутая система устойчива, то поворот того вектора относительно начала координат также будет равен .

Рассмотрим поворот вектора , он равен приращению аргумента комплекса при изменении частоты :

.

Для устойчивой в замкнутом состоянии системы

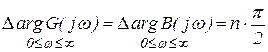
и, следовательно,

.

Если система неустойчива в замкнутом состоянии и ее характеристический полином имеет S корней в правой полуплоскости, то

при .

Если на комплексной плоскости построить годограф вектора , то годограф вектора будет соответствовать смещённой амплитудно-фазовой частотной характеристике разомкнутой системы. Для устойчивой системы результирующий угол поворота этого вектора относительно начала координат равен нулю, т.е. годограф вектора не будет охватывать начало координат.

Выполнение этого условия возможно, если амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает точку с координатами . Следовательно, для оценки устойчивости замкнутой системы достаточно построить АФЧХ разомкнутой системы и оценить её положение относительно контрольной точки с координатами . Пример построений показан на рис. 81, сплошной линией показана АФЧХ, соответствующая устойчивой в замкнутом состоянии системе, пунктирной – неустойчивой системе.

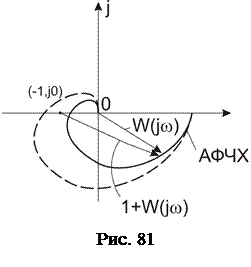Критерий Найквиста имеет следующую формулировку : если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системыамплитудно-фазовая частотная характеристика разомкнутой системы не должна охватывать на комплексной плоскости точку с координатами при изменении частоты в пределах .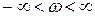

Примеры АФЧХ устойчивых систем показаны на рис. 82. Сплошной линией показана положительная ветвь АФЧХ (соответствующая ), пунктирной – отрицательная ветвь. U, V – вещественная и мнимая составляющие комплекса соответственно. В обоих случаях контрольная точка не попадает внутрь контура кривой, соответствующей годографу, что говорит об устойчивости исследуемой системы.

Для исследования устойчивости по Найквисту можно строить амплитудно-фазовую частотную характеристику только для положительных частот , поскольку ветвь для отрицательных частот является зеркальным отображением положительной ветви.

На рис. 83а показана амплитудно-фазовая частотная характеристика системы, находящейся на границе устойчивости. Признаком такого состояния системы является прохождение АФЧХ через контрольную точку . Пример АФЧХ для неустойчивой в замкнутом состоянии системы показан на рис. 83б, в этом случае контрольная точка охватывается кривой.

Если система содержит интегрирующее звено, то она становится астатической и в знаменателе передаточной функции системы появляется сомножитель p. Степень сомножителя p определяется числом интегрирующих звеньев и, в свою
очередь, определяет порядок астатизма системы. Для астатической системы с порядком астатизма передаточная функция примет вид

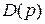где и - полиномы от p.

Частотная передаточная функция в этом случае

Можно видеть, что при 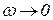A(w) будет стремиться к бесконечности. Минимальное значение фазового угла будет равно , следовательно, АФЧХ в этом случае будет представлена разомкнутой кривой.

Когда АФЧХ разомкнута, однозначно решить вопрос об охвате этой кривой контрольной точки без дополнительных соображений невозможно. Для однозначного решения вопроса об устойчивости системы в этом случае амплитудно-фазовая частотная характеристика системы дополняется полуокружностью бесконечно большого радиуса () в кратчайшем направлении к положительной вещественной полуоси, как это показано на рис. 84.

В результате этих действий кривая АФЧХ преобразуется в замкнутый контур и вопрос об охвате контрольной точки решается без затруднений. На рис. 84 замыкающая полуокружность радиуса R=¥ показана пунктиром.

Система, неустойчивая в разомкнутом состоянии, может стать устойчивой при замыкании отрицательной обратной связи. Причиной неустойчивости разомкнутой системы могут, например, быть неустойчивые местные положительные обратные связи. Для решения вопроса об устойчивости такой системы в замкнутом состоянии необходимо убедиться в наличии у знаменателя передаточной функции разомкнутой системы корней, лежащих в правой полуплоскости (т.е. с положительной вещественной частью), и определить их число k.

Критерий Найквиста для таких систем формулируется следующим образом: если система неустойчива в разомкнутом состоянии и её характеристический полином имеет k корней, лежащих в правой полуплоскости комплексной плоскости корней, то для устойчивости системы в замкнутом состоянии амплитудно-фазовая частотная характеристика разомкнутой системы должна охватывать k раз точку при изменении частоты от .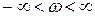

Пример амплитудно-фазовой частотной характеристики системы, которая неустойчива в разомкнутом состоянии при наличии двух правых корней характеристического полинома и становится устойчивой в замкнутом состоянии, показан на рис. 85. В рассматриваемом примере при изменении частоты вектор, проведённый из точки в текущую точку АФЧХ, поворачивается вокруг точки на угол 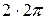, т.е. годограф охватывает точку два раза. Следовательно, в замкнутом состоянии система будет устойчивой.

Основным достоинством критерия Найквиста является его наглядность и возможность использования экспериментальных амплитудно-фазовых частотных характеристик системы в том случае, когда получение дифференциальных уравнений для системы затруднено или невозможно.

---

Дата добавления: 2015-09-02