Численное решение дифференциального уравнения

Использование ЭВМ сделало эффективным решение дифференциального уравнения численными методами. Дифференциальное уравнение переходной характеристики записывается на основе передаточной функции замкнутой системы 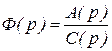и имеет следующий вид: .

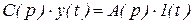Полученному уравнению соответствует структура, показанная на рис. 99а. Однако при наличии в системе дифференцирования сигнала ступенчатая функция 1 (t) в момент t=0 подвергается дифференцированию, что в ряде случаев ведет к ошибке вычисления. Чтобы обойти эту трудность, структуру целесообразно изменить в соответствии с рис. 99б.

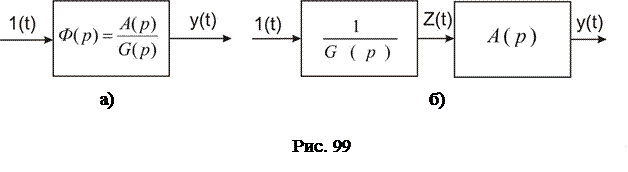
Новая структура эквивалентна предыдущей, однако свободна от ее недостатка, поскольку в этом случае ступенчатая функция вначале преобразуется инерционными, колебательными и интегрирующими звеньями, замедляющими скорость изменения сигнала при t=0.

Новой структуре соответствует система уравнений

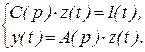
При этом первое уравнение является дифференциальным, а второе - алгебраическим, т.к. содержит производные, находимые из первого уравнения. Полученная система уравнений может быть составлена непосредственно на основе передаточной функции системы.

При численном решении дифференциального уравнения уравнение вида

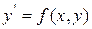с начальными условиями ,

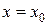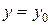
можно представить как 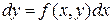или ,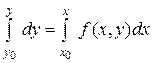

откуда .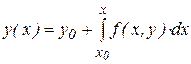

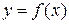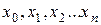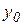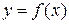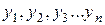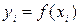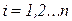Аналитическим решением уравнения является функция . Решить уравнение численным методом – это значит, для заданной последовательности аргументов и начального значения без определения найти такие значения , что , и .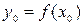

В результате получим таблицу решений исходного дифференциального уравнения для заданной последовательности значений аргумента. Величина 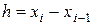- шаг интегрирования.

Для нахождения переходной характеристики необходимо решить дифференциальное уравнение порядка n

.
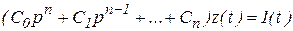Для численного решения это уравнение следует преобразовать в систему уравнений первого порядка, записанных в нормальной форме Коши, что обеспечивается выполнением подстановок 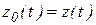, , 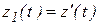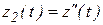…. В результате этих подстановок и с учётом связей между новыми переменными получим систему дифференциальных уравнений первого порядка:

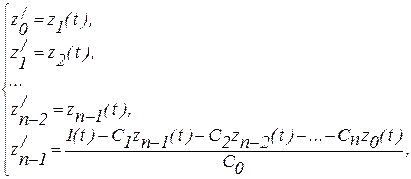
решение которой тем или иным численным методом на ЭВМ позволит получить таблицу значений величин z₀(t), z₁(t), z₂(t) … Решение для уравнения переходного процесса (переходная характеристика системы) находится через эти переменные:

.

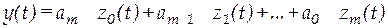При численном решении дифференциального уравнения переходной характеристики необходимо указывать начальные условия для исследуемой системы, а также определять допустимую погрешность решения, шаг интегрирования и пределы интегрирования.

При использовании ЭВМ и математического программного обеспечения численный метод оказывается наиболее простым методом.

Дата добавления: 2015-09-02