Оценка качества по распределению корней характеристического полинома системы

Метод основан на установлении связи между показателями качества переходного процесса в системе и границами распределения корней характеристического уравнения (или полинома) на комплексной плоскости.

Пусть характеристическое уравнение системы

.
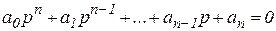Общее решение дифференциального уравнения системы для свободного процесса будет определяться корнями характеристического уравнения

,

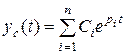где - корни характеристического уравнения (полинома), – постоянные интегрирования.

Пусть для обеспечения необходимого быстродействия системы требуется, чтобы за время выходная величина уменьшилась бы в m раз по сравнению с начальным значением. Необходимо оценить выполнение этого требования при оценке качества исследуемой системы.

Введённое ограничение означает, что корни характеристического уравнения должны не только удовлетворять условию устойчивости, но и иметь отрицательные вещественные части, по абсолютному значению не меньшие, чем величина , которая находится из условия

или .

Таким образом, для уменьшения отклонения параметра регулирования в m раз за время необходимо, чтобы все корни характеристического уравнения системы лежали бы в левой полуплоскости на расстоянии, не меньшем, чем , от мнимой оси:

.

Проверить выполнение этого условия можно либо путём построения графика распределения корней характеристического уравнения на комплексной плоскости корней, либо используя косвенные признаки.

Первый способ связан с необходимостью вычисления корней характеристического полинома системы, что в ряде случаев затруднительно. Рассмотрим способ косвенной проверки выполнения требования к вещественной части корня.

Введем новую переменную

и подставим эту переменную в исходное характеристическое уравнение, что дает

.
Раскрыв все биномы и приведя подобные члены, получим новое характеристическое уравнение (смещенное уравнение)

,

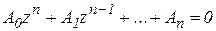где - коэффициенты, зависящие от и , и связанные с ними через биномиальные коэффициенты.

Выполнение условия устойчивости для смещённого уравнения будет соответствовать расположению корней исходного характеристического уравнения в левой полуплоскости на удалении не меньшем, чем от мнимой оси. Решить же вопрос об устойчивости смещенного характеристического уравнения можно путем применения того или иного критерия устойчивости (например, критерия Гурвица).

Величина характеризует быстродействие системы и называется степенью устойчивости системы.

Можно ввести более строгие ограничения на распределение корней характеристического полинома исходя из качества системы. Так, соотношение мнимой и вещественной частей корней характеристического полинома связано с выраженностью колебательных процессов в системе (с колебательностью системы). Если колебательность системы необходимо ограничить, то следует наложить ограничения на допустимую величину соотношения мнимой части корней характеристического полинома и вещественной части корня.

В этом случае следует ограничить угол j, в пределах которого лежат комплексные корни на комплексной плоскости корней (рис. 102). Величину называют колебательностью системы. Чем меньше величина , тем более выражен колебательный процесс и больше величина перерегулирования в системе. Исследовать в этом случае вопрос о связи между параметрами системы и расположением корней на комплексной плоскости проще всего с использованием метода D-разбиений.

Дата добавления: 2015-09-02