Интегральные оценки качества процесса

Интегральные оценки качества характеризует суммарное отклонение реального переходного процесса в системе от идеализированного переходного процесса. В качестве идеализированного процесса обычно принимается ступенчатый (скачкообразный) переходный процесс или экспоненциальный процесс с заданными параметрами экспоненты.

На рис. 103 показан пример колебательного переходного процесса в системе при подаче на вход ступенчатого сигнала. Для системы с идеальными динамическими свойствами выходной сигнал также должен измениться мгновенно и принять новое значение y_уст. Ступенчатый переходный процесс с изменением выходной величины от исходного (нулевого) значения до значения y_уст можно рассматривать как идеальный процесс, к которому должна стремиться реальная переходная характеристика системы при улучшении качества последней. Отклонение реального процесса от идеального можно рассматривать как меру качества системы автоматического управления.

Отклонение реального процесса в системе от идеального можно описать функцией отклонения (не путать с ошибкой системы)

.

Если построить график изменения во времени этого отклонения (рис. 104), то этот график будет отражать качество процесса в системе. Так, на
рис. 104 процесс, показанный пунктиром, лучше процесса, показанного сплошной линией, поскольку новое состояние системы устанавливается быстрее и интегральное отклонение процесса в системе от идеализированного ступенчатого процесса меньше.

Для численной характеристики качества процесса в системе можно принять площадь, заключённую под кривой зависимости x(t). Чем меньше эта площадь, тем выше качество процесса в системе.

Описанный подход порождает первую интегральную оценку качества системы автоматического управления

.

Для вычисления интегральной оценки нет необходимости в решении дифференциального уравнения, описывающего систему, и в нахождении функции 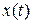. Рассмотрим более простой способ вычисления первой интегральной оценки качества системы:

.

Изображение можно найти с использованием передаточной функции системы

и

где

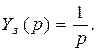
Передаточная функция замкнутой системы

,
при этом .

Следовательно,

тогда .

Полученная формула позволяет вычислить первую интегральную оценку по последним коэффициентам полиномов передаточной функции замкнутой системы. Чем меньше интегральная оценка, тем ближе реальная переходная характеристика системы к идеальной переходной характеристике (тем выше качество системы).

Первая интегральная оценка даёт адекватный результат только в случае апериодического переходного процесса в системе. В случае колебательного переходного процесса эта оценка даст заниженный результат, поскольку площадь под кривой x(t) будет содержать как положительные, так и отрицательные компоненты (рис. 105), что приведёт к занижению оценки. Для устранения указанного несоответствия наряду с первой интегральной оценкой используется и вторая интегральная оценка

.

Вычисляется вторая интегральная оценка через коэффициенты дифференциального уравнения процесса в системе или через коэффициенты полиномов в числителе и знаменателе передаточной функции замкнутой системы (что одно и то же). Пусть уравнение системы

,

где - выходной параметр системы, - входное воздействие.

Тогда вторая интегральная оценка может быть вычислена по следующим зависимостям:

,

где .

Определители ∆_к получаются из матрицы ∆ заменой столбца с номером

столбцом вида , при этом .

Коэффициенты B_i определяются по следующим формулам:

Приведенные выше формулы для вычисления второй интегральной оценки применимы, если выполняется условие .

В ряде случаев в качестве идеализированного процесса целесообразно принимать экспоненциальный процесс, а при вычислении интегральной оценки учитывать и скорость изменения ошибки. В этих случаях применяется третья интегральная оценка качества вида

,

где τ – показатель образцовой экспоненты

Интегральные оценки применяются для заведомо устойчивых систем не выше 5 порядка. Интегральные оценки не являются абсолютной характеристикой качества системы, а применяются для сравнения систем и разных вариантов системы, т.е. для сравнительной оценки систем автоматического управления. Чем меньше величина интегральной оценки, тем выше качество системы.

Поскольку свойства системы заранее могут быть неизвестными, то обычно вычисляются и первая, и вторая оценки одновременно. Для ограничения колебательности системы следует ограничивать соотношение этих оценок из следующих соображений: для систем второго порядка λ=0,8…0,9; для систем третьего порядка λ=0,7…0,8; для систем четвертого порядка λ=0,6…0,7.

---

Дата добавления: 2015-09-02