Читайте также:
|
При воздействии на вход системы гармонического сигнала
сигнал на выходе системы может быть определен через частотную передаточную функцию замкнутой системы
.
Если входной сигнал не является гармоническим, но представляет собой некоторую периодическую функцию, то ее можно разложить в ряд Фурье и рассматривать прохождение через систему каждой гармоники отдельно, а затем суммировать результаты. Периодическая функция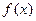 
(однозначная в пределах периода и имеющая ограниченное число разрывов и конечное число экстремумов (условия Дирихле)) раскладывается в ряд Фурье
,
где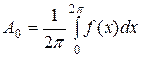 
, 
, 
,
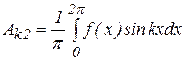- постоянная составляющая, относительно которой совершаются колебания.
В технических задачах бесконечный ряд Фурье заменяется конечным рядом, число членов которого выбирается из условия получения требуемой точности решения 
.
В теории автоматического управления рассматриваются периодические функции времени с периодом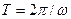 
. В этом случае ряд Фурье принимает вид
,
где 
, 
, 
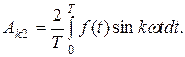
Поскольку
то ряд Фурье может быть записан в показательной форме
.
Оценка качества системы автоматического управления производится по переходному процессу при ступенчатом входном воздействии. Ступенчатая функция не является периодической. Непериодические функции можно разложить в бесконечный ряд гармоник, образующих непрерывный спектр частот. При этом 
и ряд Фурье переходит в интеграл Фурье:
,
где 
- изображение Фурье функции 
, называется также комплексным спектром функции .
С учетом свойств преобразования Фурье интеграл примет вид
.
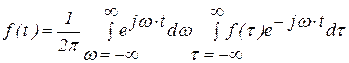Если известна частотная функция замкнутой системы 
, то переходный процесс в системе при воздействии на ее вход непериодической функции 
.
Примем 
- обобщенная частотная характеристика замкнутой системы, тогда
Подставим в выражение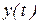 
значение 
и 
:
.
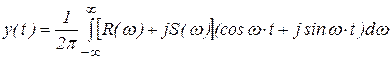При нулевых начальных условиях 
при 
, следовательно:
.
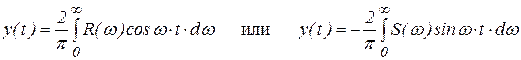Таким образом, переходный процесс в системе может быть найден по вещественной или мнимой составляющей обобщенной частотной характеристики системы автоматического управления.
Найдем обобщенную частотную характеристику при единичном входном ступенчатом воздействии. Для этого определим интеграл Фурье для единичной ступенчатой функции 
. Поскольку единичная ступенчатая функция не отвечает условиям Дирихле, то представим
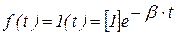при 
.
Тогда 
, откуда
.
Каждая гармоническая элементарная составляющая входного воздействия 
будет вызывать на выходе системы элементарную гармоническую составляющую процесса
.
Переходный процесс будет складываться из всех этих составляющих:
.
Представим
,
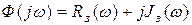где 
- вещественная частотная характеристика замкнутой системы,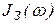 
- мнимая частотная характеристика замкнутой системы.
Учитывая нулевые начальные условия системы и преобразуя выражения, можно получить
.
Полученная формула устанавливает однозначную связь между вещественной частотной характеристикой замкнутой системы и видом переходного процесса в ней при единичном ступенчатом входном воздействии. Следовательно, вид переходной характеристики системы полностью определяется видом её частотной характеристики. Поскольку по частотной характеристике системы можно судить о её переходной характеристике, то оценку качества системы можно производить по её частотной характеристике.
Дата добавления: 2015-09-02; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегральные оценки качества процесса | | | Оценка качества системы по частотной характеристике |