Читайте также:
|
Поскольку переходная характеристика системы однозначно определяется вещественной составляющей частотной характеристики замкнутой системы
,
то по виду вещественной частотной характеристики замкнутой системы можно судить о её качестве. Для оценки качества системы необходимо построить график её вещественной частотной характеристики. Вид вещественной частотной характеристики определяется особенностями динамики системы. Для обыкновенной линейной системы частотная характеристика будет соответствовать одному из графиков, показанных на рис. 106.
График 1 соответствует невозрастающей вещественной характеристике, график 2 – монотонно убывающей характеристике, график 3 - характеристике, имеющей максимум, график 4 – знакопеременной вещественной характеристике. На основе рассмотрения вещественной частотной характеристики замкнутой системы можно сделать ряд заключений о качестве системы. Такое заключение делается на основе применения ряда правил, которые изложены ниже.
1. Приблизительно одинаковым процессам соответствуют приблизительно одинаковые частотные характеристики. Это дает возможность для оценки вида переходного процесса в системе использовать типовые характеристики.
2. При изучении системы можно ограничиться областью существенных частот (до 
), для которых ординаты 
еще значительны. Отбрасывание высокочастотных участков 
искажает переходный процесс лишь вначале.
3. Установившееся значение выходного параметра в системе при единичном входном скачкообразном воздействии
 |
4. Двум сходным вещественным частотным характеристикам, отличающимся масштабом по оси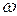 
(рис. 107, верхние графики), соответствуют похожие переходные процессы, однако переходный процесс, соответствующий "растянутой" в m раз характеристике, протекает в m раз быстрее (рис. 107, нижние графики). Следовательно, быстродействие системы будет тем выше, чем больше область частот, в которой ординаты Rз(w) имеют существенную положительную величину (чем растянутее частотная характеристика вдоль оси частот).
5. Если вещественная частотная характеристика положительна и не возрастает: 
и 
(график 1 на рис. 106), то в системе будет наблюдаться колебательный процесс, а величина перерегулирования в системе
будет не более 18 %.
6. Если зависимость монотонно убывает (график 2 на рис. 106):
, 
, 
,
то процесс в системе стремится к установившемуся значению без перерегулирования (апериодический процесс), а время переходного процесса 
. Время переходного процесса определяется по времени достижения выходной величиной значения, отличающегося не более чем на 5 % от установившейся величины.
7. Если зависимость меняет знак (график 4 на рис. 106), то время переходного процесса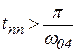 
.
8. Если зависимость положительна и имеет выраженный максимум (график 3 на рис. 106), то в системе колебательный переходный процесс с перерегулированием
,
где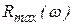 
- ордината характеристики , соответствующая максимуму.
9. Если при некотором значении частоты обращается в бесконечность (разрыв характеристики), то система является неустойчивой.
10. Длительность переходного процесса тем меньше и качество процесса тем лучше, чем более плавный характер имеет характеристика 
и чем сильнее она растянута вдоль оси частот.
Дата добавления: 2015-09-02; просмотров: 142 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основы метода | | | Оценка колебательности системы |