Оценка качества САУ по логарифмическим характеристикам

Для оценки качества системы автоматического управления используются и логарифмические частотные характеристики системы. Логарифмические частотные характеристики показаны на рис. 113: L(w) – логарифмическая амплитудная характеристика, j(w) – логарифмическая фазовая характеристика. На характеристиках можно выделить две характерные частоты: 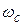- частота среза системы, 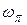- частота фазового угла, равного -p (или -180⁰).

Характер процесса в системе определяется среднечастотным участком ЛАХ, примыкающим к частоте среза 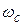системы. Плавный апериодический процесс без перерегулирования возможен только в том случае, когда наклон ЛАХ в пределах не менее ± 0,6 дек относительно частоты среза 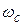равен -20 дБ/дек. В остальных случаях переходный процесс в системе будет колебательным с большей или меньшей величиной перерегулирования в зависимости от степени устойчивости системы.

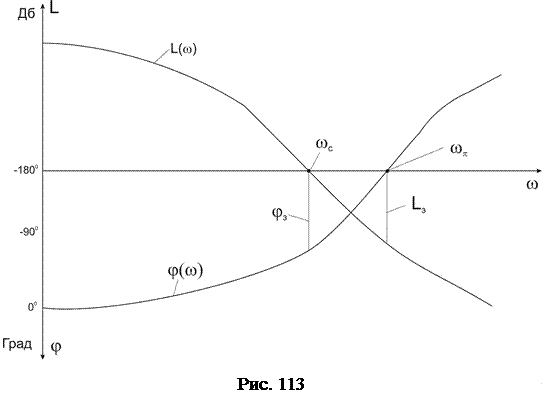
Степень устойчивости системы характеризуют показатели, определяемые по логарифмическим характеристикам и называемые запасом устойчивости системы. Различают запас устойчивости по фазе j_з и запас устойчивости по амплитуде L_з. Запас устойчивости по фазе определяется через фазовый угол системы на частоте среза w_с:

.

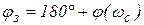Чтобы система обладала достаточным качеством, запас устойчивости по фазе должен быть не менее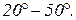

Запас устойчивости по амплитуде определяется как ордината ЛАХ на частоте фазового угла, равного -p:

.

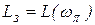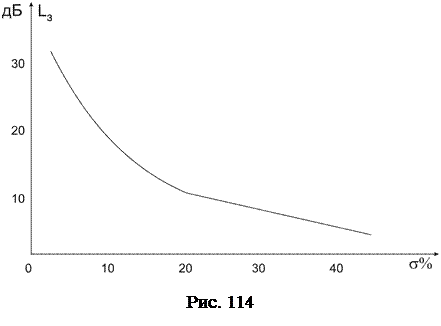Эта величина связана с перерегулированием в системе. Перерегулиро-вание будет тем больше, чем меньше запас устойчивости по амплитуде. Связь между величиной перерегулирования и запасом устойчивости по амплитуде характеризуется графиком на рис. 114. При запасе устойчивости по амплитуде менее -10 дБ перерегулирование в системе может превысить 40 %. Для обеспечения перерегулирования в системе не более 20 % запас по амплитуде должен быть не менее -15 ∂Б.

Частота среза системы определяет её быстродействие. Чем выше частота среза, тем меньше длительность переходного процесса в системе. Для системы удовлетворительного качества в первом приближении длительность t_п переходного процесса связана с частотой среза системы следующей зависимостью:

.

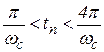По логарифмическим характеристикам можно оценить и колебательность системы с применением показателя колебательности 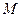. Пусть частотная передаточная функция разомкнутой системы 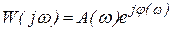. Тогда для некоторого значения модуля A связь между запасом устойчивости по фазе j_з и показателем колебательности системы M определится соотношением

.

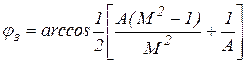Приведенное выше соотношение используется для значений модуля АФЧХ, лежащих в пределах

,

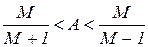так как при иной амплитуде 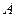запас по фазе может быть любым.

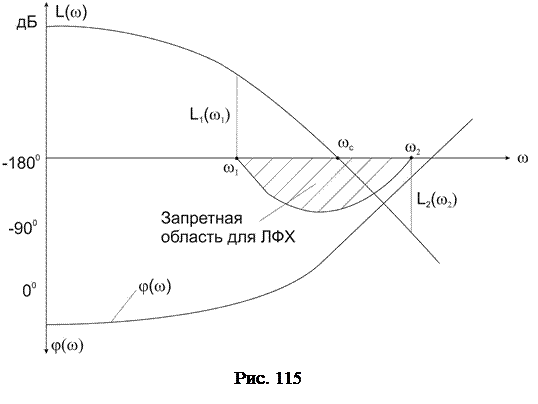
При оценке колебательности системы по логарифмическим характеристикам задается предельное значение показателя колебательности системы и проверяется условие отсутствия превышения фактического показателя колебательности системы введённого ограничения. Если условие не выполняется, то качество системы по колебательности считается неудовлетворительным.

Для проверки условия при заданном показателе колебательности 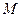прежде всего вычисляются две ординаты ЛАХ, соответствующие ограничениям на модуль частотной характеристики:

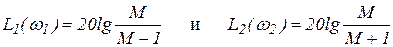. Для этих ординат .

Затем на графике ЛАХ определяется ряд ординат L(w), лежащих между значениям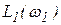и и 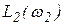(берётся ряд частот в интервале от w₁ до w₂) и для каждой ординаты вычисляется требуемый запас устойчивости по фазе

, .

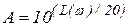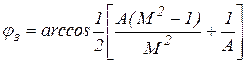На графике логарифмических характеристик строится полученная зависимость 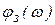(рис. 115). В результате формируется запретная область для ЛФХ системы. Чтобы система имела показатель колебательности не больше, чем заданная величина , ЛФХ системы не должна заходить в запретную область.

Дата добавления: 2015-09-02