Интеграл как функция верхнего предела.

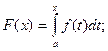Теорема 4.1. Пусть Рассмотрим функцию имеет место равенство

Доказательство. Функция 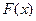существует, так как . Имеем

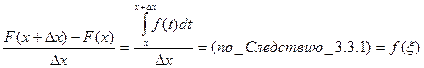, где точка ; если , а , по непрерывности. Теорема доказана.

Таким образом, для непрерывной функции 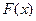- первообразная для .

Теорема 4.2. Пусть - любая первообразная для на . Тогда

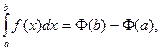
если .

Доказательство. В условиях теоремы, 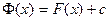для некоторой константы 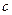, где

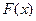определена как в предыдущей теореме. Имеем, далее,

Теорема доказана.

Эта теорема позволяет вычислять определённые интегралы через значения первообразных (и тем самым в некотором смысле оправдывает введение понятия первообразной). Можно слегка обобщить её.

Теорема 4.3. Пусть , исключая конечное число точек внутри отрезка.

Тогда , где функция 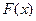в точках разрыва определена произвольно, а между ними – как первообразная для на соответствующем промежутке.

Ни уточнять, ни доказывать мы её не будем.

Теорема 4.4. (Вторая теорема о среднем). Пусть функция 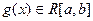, а на

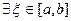монотонна. Тогда , такая, что .

Лемма 4.3.1. (Формулы Бонне).Если на функция не возрастает и неотрицательна, а 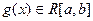, то 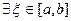, для которой

.

Аналогично, если на 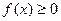и не убывает, а 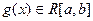, то 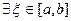такая, что

. , где .

Доказательство. Докажем первую часть. Разобьём отрезок на более мелкие точками 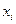.Имеем:

Вторая сумма будет стремиться к 0 при мелкости разбиения стремящейся к 0, потому что второй сомножитель под интегралом ограничен,а первый – это колебание функции на 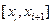, и сумма будет стремиться к нулю, так как .

Значит, первая сумма будет стремиться к интегралу. Положим 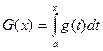. Имеем:

.

Функция 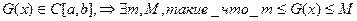, следовательно, поскольку все разности неотрицательны, , и , где . В силу непрерывности , , , что даёт первую из формул. Вторая доказывается аналогично.

Доказательство теоремы. Пусть монотонно убывает. В первой формуле Бонне возьмём вместо разность . После преобразований (формальных и не связанных с новыми идеями) получим утверждение теоремы.

Примечание. Эта теорема в лекционном курсе не доказывалась.

Дата добавления: 2015-08-26