
|
Читайте также: |
Доказательство. Рассмотрим две последовательности: последовательность левых концов,  , и последовательность правых концов,
, и последовательность правых концов, 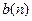 .Первая из них неубывающая и ограниченная сверху, вторая – невозрастающая и ограниченная снизу. По предыдущему следствию, обе они имеют пределы
.Первая из них неубывающая и ограниченная сверху, вторая – невозрастающая и ограниченная снизу. По предыдущему следствию, обе они имеют пределы  и
и  , соответственно. Поскольку для любого
, соответственно. Поскольку для любого  и для любого
и для любого  всегда будет
всегда будет  , то будут выполняться и неравенства
, то будут выполняться и неравенства  и
и  .Следовательно,
.Следовательно,  .В частности, при
.В частности, при  получим
получим  , откуда
, откуда  .Предел выражения справа равен 0 по условию. Значит,
.Предел выражения справа равен 0 по условию. Значит,  . Лемма доказана.
. Лемма доказана.
Примечание 1. Леммы 2.1.7 и 2.1.8 эквивалентны основной Аксиоме.
Примечание 2. Если в условии Леммы заменить отрезки на интервалы или полуинтервалы, её утверждение, вообще говоря, не будет иметь места. Если же отказаться от условия (3), то общих точек будет много, целый отрезок 
2.2.Последовательности, не имеющие предела.
Определение 2.5. Точка  называется предельной точкой последовательности
называется предельной точкой последовательности  (множества
(множества  ), если в любой проколотой окрестности этой точки есть хотя бы один элемент последовательности
), если в любой проколотой окрестности этой точки есть хотя бы один элемент последовательности  (множества
(множества  ).
).
Определение 2.6. Точка  называется изолированной точкой множества
называется изолированной точкой множества  , если она принадлежит множеству
, если она принадлежит множеству  и если существует окрестность точки
и если существует окрестность точки  , в которой нет других точек множества
, в которой нет других точек множества  .
.
Примеры: (1) У последовательности  все точки – изолированные.
все точки – изолированные.
(2) У последовательности 1;1;2;1:3;1;4;…… точка 1 является предельной.
Лемма 2.2.1. Всякая ограниченная последовательность имеет хотя бы одну предельную точку, и существует подпоследовательность, сходящаяся к этой точке.
Доказательство. Оба утверждения будут доказываться вместе. Пусть  - рассматриваемая последовательность. Она по условию ограничена, значит у неё существуют конечные точные грани, нижняя -
- рассматриваемая последовательность. Она по условию ограничена, значит у неё существуют конечные точные грани, нижняя -  , и верхняя -
, и верхняя -  . Все элементы
. Все элементы  лежат на отрезке
лежат на отрезке 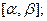 поделим его пополам. Хотя бы на одной из половин будет лежать бесконечное число элементов последовательности
поделим его пополам. Хотя бы на одной из половин будет лежать бесконечное число элементов последовательности  (в противном случае их число было бы конечным на всём
(в противном случае их число было бы конечным на всём  ). Из элементов, лежащих на этой половине, произвольно выберем какой-нибудь, например,
). Из элементов, лежащих на этой половине, произвольно выберем какой-нибудь, например, 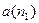 . Концы этой половины обозначим (слева направо!)
. Концы этой половины обозначим (слева направо!)  .Поделим выбранную половину отрезка опять пополам. На одной из двух образовавшихся половин (четвертинок первоначального
.Поделим выбранную половину отрезка опять пополам. На одной из двух образовавшихся половин (четвертинок первоначального  ) опять окажется бесконечное число элементов
) опять окажется бесконечное число элементов  . Выберем среди них элемент
. Выберем среди них элемент  так чтобы было
так чтобы было  , обозначим концы выбранной половинки
, обозначим концы выбранной половинки  и продолжим деление пополам. Те половинки, которые мы выбираем, образуют систему стягивающихся отрезков
и продолжим деление пополам. Те половинки, которые мы выбираем, образуют систему стягивающихся отрезков  , по длине стремящихся к 0. У них, по Лемме о стягивающихся отрезках, есть общая точка
, по длине стремящихся к 0. У них, по Лемме о стягивающихся отрезках, есть общая точка  . Элементы
. Элементы 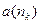 , которые мы выбирали, образуют подпоследовательность последовательности
, которые мы выбирали, образуют подпоследовательность последовательности  ,так как номера
,так как номера 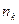 возрастают. Покажем, что
возрастают. Покажем, что  - предел этой подпоследовательности. Если
- предел этой подпоследовательности. Если 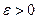 выбрано произвольно, мы всегда можем указать номер
выбрано произвольно, мы всегда можем указать номер  , для которого длина очередной половинки будет меньше, чем
, для которого длина очередной половинки будет меньше, чем 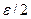 .Так как
.Так как  и
и 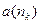 лежат на этой половинке, и все последующие
лежат на этой половинке, и все последующие  для
для  будут лежать там же, то неравенство
будут лежать там же, то неравенство  будет выполняться для всех
будет выполняться для всех  Значит,
Значит,  . В любой проколотой окрестности точки
. В любой проколотой окрестности точки  будет содержаться хотя бы одна точка последовательности
будет содержаться хотя бы одна точка последовательности  (в силу правила выбора половинок отрезков). Значит,
(в силу правила выбора половинок отрезков). Значит,  будет предельной точкой последовательности
будет предельной точкой последовательности 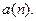
Лемма доказана.
Если последовательность  не ограничена, она может не иметь предельных точек:
не ограничена, она может не иметь предельных точек:
(1)  , или (2) иметь:
, или (2) иметь: 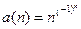 . В случае (2) предельных точек может быть сколько угодно (например, вся числовая прямая, то есть все действительные числа могут быть предельными точками одной последовательности). Для ограниченных последовательностей предельные точки могут иметься в любом конечном количестве, или их число может быть бесконечным, в частности, они могут заполнять отрезок, полуинтервал или интервал.
. В случае (2) предельных точек может быть сколько угодно (например, вся числовая прямая, то есть все действительные числа могут быть предельными точками одной последовательности). Для ограниченных последовательностей предельные точки могут иметься в любом конечном количестве, или их число может быть бесконечным, в частности, они могут заполнять отрезок, полуинтервал или интервал.
Определение 2.7. Точная нижняя грань множества предельных точек последовательности  (конечная или бесконечная) называется нижним пределом последовательности
(конечная или бесконечная) называется нижним пределом последовательности  и обозначается
и обозначается  ; точная верхняя грань множества предельных точек последовательности
; точная верхняя грань множества предельных точек последовательности  (конечная или бесконечная) называется верхним пределом последовательности
(конечная или бесконечная) называется верхним пределом последовательности  и обозначается
и обозначается  .
.
Примеры:1.У последовательности 
 ;2.У последовательности
;2.У последовательности 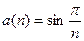
 ;3.У последовательности
;3.У последовательности 
 .
.
Лемма 2.2.2.(Критерий Коши). Для того чтобы последовательность  сходилась, необходимо и достаточно, чтобы для неё выполнялось следующее условие(условие Коши): для всякого
сходилась, необходимо и достаточно, чтобы для неё выполнялось следующее условие(условие Коши): для всякого 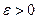 существует
существует  , такое, что для любых
, такое, что для любых 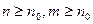 имеет место неравенство
имеет место неравенство  .
.
Доказательство. (1) Необходимость: если последовательность  сходится, условие выполняется. Если
сходится, условие выполняется. Если  , то по
, то по 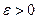 найдётся такой номер
найдётся такой номер  , что для всех
, что для всех 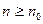 будет выполняться неравенство
будет выполняться неравенство 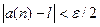 .Для любых
.Для любых 
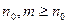 будем иметь
будем иметь
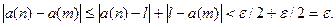 Условие выполнено.
Условие выполнено.
(2) Достаточность. Если условие выполнено, последовательность сходится. Пусть условие выполнено. Возьмём какое-нибудь 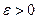 , найдём по нему
, найдём по нему  .Тогда для всех
.Тогда для всех 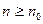 будет выполняться неравенство
будет выполняться неравенство  или
или 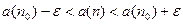 . Отсюда следует, что
. Отсюда следует, что  ограничена (так как вне интервала
ограничена (так как вне интервала  находится конечное число членов последовательности). Поскольку
находится конечное число членов последовательности). Поскольку  ограничена, у неё есть предельные точки. Если предельная точка всего одна, то это и есть
ограничена, у неё есть предельные точки. Если предельная точка всего одна, то это и есть  .(Почему?) Предположим, что есть две разных предельных точки,
.(Почему?) Предположим, что есть две разных предельных точки,  . Возьмём
. Возьмём 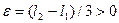 . Существуют подпоследовательности последовательности
. Существуют подпоследовательности последовательности  сходящиеся к этим предельным точкам. Пусть подпоследовательность
сходящиеся к этим предельным точкам. Пусть подпоследовательность  сходится к
сходится к  , а подпоследовательность
, а подпоследовательность  - к
- к  .По выбранному
.По выбранному 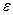 , из условия Коши найдём
, из условия Коши найдём  , такое что для всех
, такое что для всех 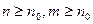
 ; найдутся также
; найдутся также  и
и  , такие что для
, такие что для  и
и  будут выполняться неравенства
будут выполняться неравенства 
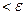 и
и 
 , соответственно. Имеем
, соответственно. Имеем
 если
если 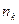 и
и 
 будут не меньше
будут не меньше  . Полученное противоречие показывает, что предельная точка у нашей последовательности всего одна. Лемма доказана.
. Полученное противоречие показывает, что предельная точка у нашей последовательности всего одна. Лемма доказана.
Примечание. Критерий Коши эквивалентен основной Аксиоме.

3.Предел функции
Пусть имеется функция  f(x), определённая в проколотой окрестности
f(x), определённая в проколотой окрестности  U(x
U(x  ) (или в одной из полуокрестностей).
) (или в одной из полуокрестностей).
Определение 3.1. Пределом функции f(x) в точке x называется число A,если для всякого 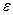 >0 найдётся
>0 найдётся 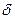 >0,такое, что для всех x из U
>0,такое, что для всех x из U 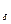 (x
(x  ),x
),x  x
x  ,
,  .
.
Это определение называется определением предела функции по Коши.
Другие формулировки. 1. Обозначение  . 2. Говорят, что предел функции
. 2. Говорят, что предел функции  равен A при стремлении точки x к точке
равен A при стремлении точки x к точке  , если при стремлении к нулю
, если при стремлении к нулю
разности x-x  стремится к нулю разность f(x) – A. 3. A = lim
стремится к нулю разность f(x) – A. 3. A = lim 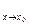 f(x), если для всякого
f(x), если для всякого 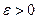 найдётся такое
найдётся такое 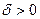 , что для всех x
, что для всех x  x
x  ,для которых выполняются неравенства
,для которых выполняются неравенства 
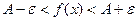 ,будут выполняться неравенства
,будут выполняться неравенства 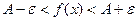 .
.
4.  .
.
5.  (
(
 )
) 
 .Символом U
.Символом U  обозначается проколотая окрестность.
обозначается проколотая окрестность.
Определение 3.2. Число A называется пределом функции  ,определённой в некоторой проколотой окрестности точки
,определённой в некоторой проколотой окрестности точки  ,если для любой последовательности точек
,если для любой последовательности точек  ,принадлежащей указанной окрестности и сходящейся к
,принадлежащей указанной окрестности и сходящейся к  , последовательность значений функции
, последовательность значений функции  сходится к A.
сходится к A.
Это определение предела называется определением предела функции по Гейне.
Теорема 3.1. Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство. 1.Пусть  по Коши. Тогда для любого
по Коши. Тогда для любого 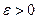 найдётся
найдётся 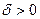 , такое, что
, такое, что  для всех
для всех  Пусть теперь
Пусть теперь  - произвольная последовательность, сходящаяся к точке
- произвольная последовательность, сходящаяся к точке  Согласно определению предела последовательности, найдётся такое
Согласно определению предела последовательности, найдётся такое  что при
что при 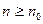 всегда будет
всегда будет  Поэтому, начиная с
Поэтому, начиная с  ,будет выполняться неравенство
,будет выполняться неравенство  , и мы получили:
, и мы получили:  Значит
Значит  - предел
- предел  по Гейне.
по Гейне.
2.Пусть теперь  по Гейне. Предположим, что
по Гейне. Предположим, что  по Коши. Тогда найдётся
по Коши. Тогда найдётся 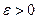 , такое, что для любого 1>
, такое, что для любого 1> 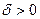 найдётся такой
найдётся такой  , что с одной стороны,
, что с одной стороны,  а с другой стороны,
а с другой стороны,  Множество точек
Множество точек  является ограниченным: оно всё принадлежит окрестности
является ограниченным: оно всё принадлежит окрестности 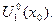 Пусть
Пусть  .Тогда
.Тогда  но
но  и, значит,
и, значит, 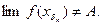 Мы нашли последовательность, сходящуюся к
Мы нашли последовательность, сходящуюся к  и такую, что соответствующая последовательность значений функции
и такую, что соответствующая последовательность значений функции  не сходится к
не сходится к  Это противоречит предположению, что
Это противоречит предположению, что  - предел
- предел  по Гейне.
по Гейне.
Теорема доказана.
Следствие 3.1. Леммы 2.1.1 – 2.1.8 справедливы для функций, имеющих предел в точке, при соответствующей переформулировке. А именно
3.1.1. Если  то найдётся окрестность точки
то найдётся окрестность точки  в которой значение
в которой значение  отличается от
отличается от  менее, чем на
менее, чем на 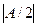 ; в частности, знак
; в частности, знак  для всех
для всех 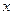 из этой окрестности будет совпадать со знаком
из этой окрестности будет совпадать со знаком 
3.1.2. Если  то
то  ,в которой
,в которой  ограничена.
ограничена.
3.1.3. Пусть в некоторой окрестности  функция
функция  - бесконечномалая при
- бесконечномалая при  ,
,  - ограниченная.
- ограниченная.  Тогда
Тогда  - бесконечномалая. Сумма конечного числа бесконечномалых есть функция бесконечномалая. Модуль бесконечномалой функции – бесконечно
- бесконечномалая. Сумма конечного числа бесконечномалых есть функция бесконечномалая. Модуль бесконечномалой функции – бесконечно 
 малая.
малая.
3.1.4. Если  то
то 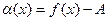 - бесконечномалая функция при
- бесконечномалая функция при 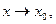 и обратно.
и обратно.
3.1.5. Пусть  . Тогда
. Тогда 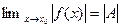 ;
;  если
если 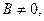 то
то 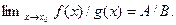
3.1.6. Если в некоторой окрестности 
 и
и  то
то 
3.1.7. Если в некоторой окрестности 
 и
и  , то
, то 
3.1.8. Пусть при 
 монотонно возрастает и ограничена. Тогда
монотонно возрастает и ограничена. Тогда 
3.2.Критерий Коши для функций. Пусть  определена в некоторой
определена в некоторой  .Для того, чтобы существовал
.Для того, чтобы существовал  , необходимо и достаточно, чтобы для любого
, необходимо и достаточно, чтобы для любого 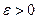 нашлось
нашлось 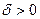 такое, что для любых
такое, что для любых 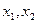 из
из  ,для которых
,для которых  , выполнялось неравенство
, выполнялось неравенство 
Все эти утверждения доказываются либо непосредственно из определения предела функции, либо ссылкой на то, что аналогичные утверждения верны для последовательностей и Теорему 3.1.
Докажем, например,3.1.8.Пусть выполнены условия 3.1.8,и пусть  монотонно возрастая. Тогда
монотонно возрастая. Тогда  монотонно возрастает и ограничена сверху, и, значит, имеет предел А. Пусть
монотонно возрастает и ограничена сверху, и, значит, имеет предел А. Пусть 
 ,
, 
 для всех
для всех  ,тоже монотонно возрастая. Тогда последовательность
,тоже монотонно возрастая. Тогда последовательность  тоже будет монотонно возрастающей и ограниченной и, значит, будет иметь предел В. Но
тоже будет монотонно возрастающей и ограниченной и, значит, будет иметь предел В. Но  такое, что
такое, что  ,и,значит,
,и,значит,  ,откуда
,откуда  .По аналогичной причине,
.По аналогичной причине,  .Следовательно,
.Следовательно,  , и всё доказано.(Почему? Что будет, если
, и всё доказано.(Почему? Что будет, если  , не монотонно?)
, не монотонно?)
Дата добавления: 2015-08-26; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ 1 страница | | | ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ 3 страница |