Введение в математический анализ 5 страница

Теорема 7.2. Для того, чтобы дифференцируемая функция была выпуклой на промежутке , необходимо и достаточно, чтобы её первая производная не убывала.

Доказательство. Если функция выпуклая, то устремляя 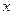в основном неравенстве сначала к , а потом к , получим .

Наоборот, если выполнено неравенство , пусть .Если на всём 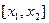производная равна константе, то основное неравенство выполняется. Если производные не равны, то,по теореме Лагранжа, имеем

, где . По предположению, , и мы получили основное неравенство. Теорема доказана.

Теорема 7.3. Для того, чтобы функция была строго выпуклой на промежутке, достаточно, чтобы её производная строго возрастала.

Для доказательства следует только обратить внимание на то, что в предыдущем доказательстве, в условиях теоремы 7.2, всегда будет .

Теорема 7.4. Для того, чтобы дважды дифференцируемая на промежутке функция была выпуклой, необходимо и достаточно, чтобы её вторая производная была неотрицательной.

Очевидно, так как условие означает, что производная первая не убывает.

Теорема 7.5. Для того, чтобы дважды дифференцируемая функция была строго выпуклой, достаточно, чтобы её вторая производная была положительной.

В этом случае первая производная строго возрастает.

Теорема 7.6. Для того, чтобы функция была выпуклой, необходимо и достаточно, чтобы в любой точке её график лежал не ниже касательной.

Доказательство. Если функция в точке лежит выше касательной, то имеет место неравенство

.Если 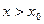, оно означает, что , если , неравенство будет в обратную сторону. То есть, для любых 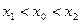будет

- основное неравенство. Значит, функция выпуклая.

Наоборот, если функция выпуклая, то для любых 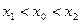выполняется неравенство

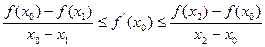, которое эквивалентно утверждению, что функция лежит выше касательной. Теорема доказана.

8. Дополнительные сведения о свойствах дифференцируемых функций

Теорема 8.1. (Дарбу). Пусть . Если , то , для которой .

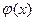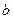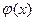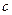Доказательство. Положим . Тогда . Пусть, для определённости, . Тогда правее точки убывает, левее точки - возрастает. Значит, минимум функции достигается внутри интервала в некоторой точке . Очевидно, функция 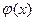дифференцируема в точке 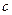и некоторой её окрестности. Следовательно, и теорема доказана.

Таким образом, для производных верен аналог теоремы Коши для непрерывных функций.

Рассмотрим теперь вопрос о непрерывности прозводной.

Из теоремы Лагранжа следует, что если . Пусть при этих предположениях . Тогда

. Пусть .Тогда .Выражение слева будет стремиться к , и предел правого выражения тоже будет равен . Однако предел может при этом существовать, в этом случае производная будет непрерывна в точке .Но он может и не существовать, как показывает пример функции .Таким образом, верна

Теорема 8.2. (о разрывах производных). Если функция , то в любой точке этого интервала её производная либо непрерывна, либо имеет разрыв второго рода (в разных точках по-разному).

Дата добавления: 2015-08-26