Классы интегрируемых функций

3.1.Функция Дирихле не интегрируема.

Действительно, на отрезке при 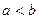верхняя сумма Дарбу всегда будет равна 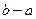, а нижняя – 0.

3.2.Если .

Доказательство. Если , то для будет либо

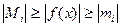, либо неравенства будут в обратную сторону. В любом случае,

будет не меньше, чем аналогичная разность для модуля функции. Следовательно, разность верхней и нижней сумм для модуля функции не будет превосходить аналогичную разность для самой функции. Если 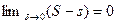, то то же самое будет верно и для модуля функции. Утверждение доказано.

3.3.Первая (простая) теорема о среднем. Если , то , где .

Доказательство. Очевидно, 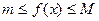. Проинтегрируем

. Теорема доказана. ().

Следствие 3.3.1. Если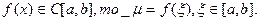

3.4.Теорема 3.4.1. Если , то она интегрируема на этом отрезке.

Доказательство. По теореме Кантора, равномерно непрерывна на .

По выберем 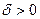так, чтобы при .Тогда получим

.

Теорема 3.4.2. Если ограниченная функция определена и монотонная на отрезке, она

на нём интегрируема.

Доказательство. Пусть, для определенности, функция на монотонно возрастает. По выберем . Тогда .

Теорема доказана.

Теорема 3.4.3. Ограниченная на отрезке функция, имеющая на нём конечное число точек разрыва, интегрируема.

Докажем эту теорему для случая, когда точка разрыва одна. Общий случай доказывается аналогично. Пусть .При любом разбиении отрезка, точка разрыва 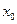будет принадлежать не более, чем двум отрезкам разбиения. Если мелкость разбиения равна 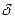, вклад этих максимум двух отрезков разбиения в разность сумм Дарбу будет не более . На оставшейся части отрезка функция интегрируема, и по можно выбрать такое , что разность сумм Дарбу там будет меньше .Пусть и .Разность сумм Дарбу на всём отрезке будет меньше 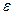. Теорема доказана.

Теорема 3.4.4. Если функция 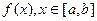, интегрируема, то будет интегрируемой и функция, полученная из произвольным изменением её значений в конечном числе точек.

Доказательство. Аналогично предыдущему доказательству, разница в значении сумм Дарбу для новой функции сколь угодно мало отличается от значений сумм Дарбу для исходной функции.

Обе эти теоремы могут быть получены как тривиальное следствие следующей теоремы Лебега об интегрируемости функций по Риману.

Определение 3.1.Множество точек числовой оси называется множеством меры 0, если его можно накрыть системой окрестностей общая длина которых может быть сделана меньше любого (т.е., для любого .найдётся система окрестностей, накрывающая все точки множества, с общей суммой длин меньшей .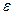

Примеры. 1.Любое конечное множество точек имеет меру 0.

2. Любое счётное множество имеет меру 0.

3. Существуют несчётные множества, имеющие меру 0.

Теорема 3.4.5. Для того, чтобы функция была интегрируема по Риману на отрезке, необходимо и достаточно, чтобы мера множества точек разрыва этой функции была равна 0.

Доказывается она примерно так же, как две предыдущих.

Теорема 3.4.6. Пусть функция интегрируема на наибольшем из отрезков

. Тогда она интегрируема на двух остальных отрезках, и

.

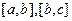Если интегрируема на , то она интегрируема и на .

Доказательство. Для простоты докажем всё для случая .

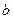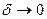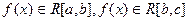Если , то , если рассматривать разбиения отрезка , содержащие точку .Поскольку предположено, что , левая часть будет произвольно мала при , значит и правая – тоже. Для отрезка - аналогично. Если , то любую интегральную сумму для можно, добавив, может быть, точку 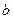к точкам разбиения, представить в виде суммы интегральных сумм для 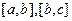. Произвольная интегральная сумма будет отличаться от получившейся сколь угодно мало. Следовательно, .

Из последнего замечания вытекает и нужное равенство. Теорема доказана.

Теорема 3.4.7. Если , то .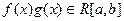

Доказательство. Пусть на отрезке . Имеем

Если мы возьмём какое-нибудь разбиение отрезка , это неравенство будет выполняться для любых из любого отрезка разбиения . Пусть соответственно, - колебания функций на . Имеем

. Умножая на и суммируя, получим

; последние две суммы стремятся к нулю при измельчении отрезка в силу интегрируемости функций .

Теорема доказана.

Дата добавления: 2015-08-26