Интегралы

1 .Неопределённый интеграл и первообразная

Определение 1.1. Пусть функция определена на отрезке .Функция 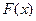называется первообразной для функции на отрезке , если . Вместо отрезка можно взять любой промежуток .

Пусть 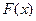- первообразная для на . Тогда и , будет первообразной для на том же отрезке.

Пусть теперь - две любых первообразных для на отрезке .Тогда

.Как следует из теоремы Лагранжа, это означает, что , где - некоторая фиксированная для всего отрезка константа.

Мы только что доказали, что

Теорема 1.1 Для того, чтобы две функции были первообразными для одной функции на отрезке , необходимо и достаточно, чтобы они различались на константу.

Определение 1.2. Совокупность всех первообразных функции на отрезке называется неопределённым интегралом функции на отрезке и обозначается .

Если 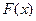- какая-нибудь первообразная для , то где - произвольная константа.

2.Свойства неопределённых интегралов.

Все свойства неопределённых интегралов вытекают из определения. Для их проверки (или доказательства) достаточно продифференцировать правую и левую части соответствующего равенства; если результаты совпадут, равенство верное.

2.1. , если интегралы справа существуют;

2.2. , где - произвольная постоянная; если , то

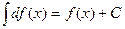и

2.3.(Замена переменной) Если , то

2.4. (Правило интегрирования по частям) , если ;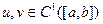

2.5. Стандартная таблица простейших неопределённых интегралов:

1. ,если ;

2.

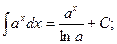
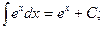
3.

4.

5.

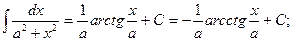
6.

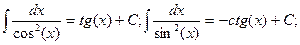
7.

8.

3. Можно заметить, что в стандартную таблицу не попали некоторые интегралы от простейших элементарных функций. Это произошло по двум причинам.

Во-первых, интегралы от логарифма, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса легко вычисляются через приведённые. Во-вторых, в простейших случаях интеграл , где - простейшие элементарные функции

не выражается в конечном виде через простейшие элементарные функции(например,

).

Когда приходится вычислять (говорят: брать) интеграл от функции, которую Вы видите в первый раз, не факт, что Вам удастся подобрать такую конечную комбинацию элементарных функций, производной которой является подинтегральная функция.

Обычно, если сразу не видно, как свести предложенный интеграл к табличному, нужно попытаться упростить его, либо разбив на сумму более простых, либо испробовав какую-либо замену переменных. Часто встречающимися в задачниках заменами являются такие:

и так далее. Нужно помнить, что вместе с 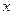следует через новую переменную заменять и .Известно несколько типов интегралов,

которые всегда выражаются в конечном виде через элементарные функции. Некоторые из них приведены ниже.

3.1. Рациональные дроби от одной переменной.

Так называются дроби вида

, где числитель – многочлен степени от 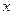, знаменатель – многочлен степени от 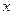. Нас будет интересовать случай . Если это неравенство не выполняется, можно разделить числитель на знаменатель с остатком. Для остатка это неравенство будет выполняться.

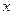По одной из основных теорем алгебры, всякий многочлен от одной переменной с действительными коэффициентами может быть однозначно разложен в произведение

, где все коэффициенты - действительные числа, - все действительные корни этого многочлена, каждый со своей кратностью , а все квадратные трёхчлены не имеют действительных корней.

Для доказательства возможности выражения неопределённого интеграла от рациональной дроби в конечном виде через элементарные функции имеют значение следующие три факта. (1)Всякую правильную(с ) рациональную дробь можно разложить на простейшие; (2) Каждой скобке вида при этом разложении соответствует набор дробей

, а каждой скобке вида - набор дробей ; (3)Интеграл от дроби сводится к сумме рациональной дроби с интегралом от .

(Подробности можно посмотреть в «толстом» Фихтенгольце).Таким образом, интеграл от всякой рациональной дроби может быть выражен в виде суммы рациональной функции, логарифмов и арктангенсов в конечном числе.

3.2. Всякая рациональная функция от тригонометрических функций может быть приведена к обычной рациональной заменой ; при замене в интеграле , .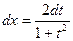

3.3. Рациональную функцию от можно свести к обычной рациональной одной из замен Эйлера.

(1).Если 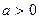, можно сделать замену 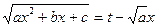; тогда , и выражается через рационально.

(2). Если , положим .

(3). Если подкоренное выражение имеет различные действительные корни , положим

.

4. Вопросами о том, что делать, если интеграл не выражается в конечном виде через элементарные функции, мы заниматься не будем.

Дата добавления: 2015-08-26