Несобственные интегралы. Введение.

5.1 Рассмотрим интеграл 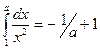. Геометрически он представляет площадь, ограниченную осью Ох, прямыми х=1 и х=а и кривой 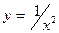. Рассмотрим . Этот предел называется несобственным интегралом первого рода от функции 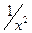на промежутке 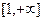и обозначается .

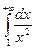Определение 5.1. Пусть функция 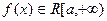. Если существует 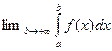, то он называется несобственным интегралом первого рода и обозначается .

Определение 5.2. Пусть функция и существует 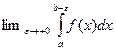. Он называется несобственным интегралом второго рода и обозначается 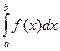.(Бесконечность может быть любого знака).

Отметим, что это, несмотря на обозначение, не обычный интеграл, потому что подинтегральная функция стремится к бесконечности в точке .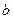

Реально встречаются несобственные интегралы, которые имеют особенности и первого и второго рода одновременно. Их изучение сводится к тому, что пространство интегрирования разбивается на промежутки, в каждом из которых содержится не более одной особенности (то есть, либо единственная точка, где функция не ограничена, либо 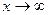в одно из концов).

Легко проверить, что подстановка вида 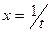превращает интеграл первого рода в интеграл второго рода, а подстановка 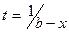- интеграл второго рода в интеграл первого рода. Будем по этой причине рассматривать интегралы первого рода, а для интегралов второго рода только приводить результаты.

Если несобственный интеграл существует, говорят, что он сходится, в противном случае – расходится.

Теорема 5.1. Сходящиеся на несобственные интегралы образуют линейное пространство.

Доказательство является следствием того обстоятельства, что функции, имеющие предел в точке, образуют линейное пространство

().

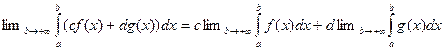Теорема 5.2.(Критерий Коши) Для того, чтобы несобственный интеграл первого рода

сходился, необходимо и достаточно, чтобы .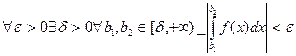

Доказательство. Это критерий Коши для функции при .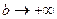

Определение 5.3. Говорят, что несобственный интеграл сходится абсолютно, если сходится интеграл (для интегралов второго рода пределы нужно изменить соответственно).

Если несобственный интеграл сходится, но не абсолютно, говорят, что он сходится условно.

Теорема 5.3. Абсолютно сходящийся интеграл сходится.

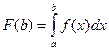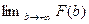Доказательство. Рассмотрим функцию и .Этот предел будет существовать, если выполнен критерий Коши, т.е., если по произвольному найдётся 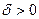, такое, что для всех будет выполняться неравенство 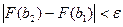. Переходя к интегралам, получим 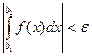. По условию, по тому же 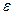можно подобрать 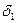, такое, что для любых 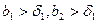будет выполняться неравенство (по тому же критерию Коши) .Возьмём 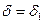; согласно неравенству 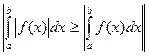, тогда будет выполняться и нужное нам неравенство. Значит, по критерию Коши будет сходиться и исходный интеграл .Теорема доказана.

Дата добавления: 2015-08-26