Функции нескольких переменных

Введение.

Мы будем рассматривать функции 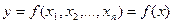, где 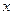будет меняться по некоторой области пространства 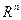. Основным понятием, которое мы использовали для получения результатов для функций одной переменной, было понятие предела функции в точке и всё, с ним связанное. При доказательствах теорем о пределах использовались свойства модуля действительных чисел, а именно следующие: (1) ;

(2) ; (3) . Сейчас мы введём понятие, аналогичное понятию модуля, для точек из 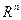. Это можно сделать разными способами. Приведём три из них, хотя существуют и другие.

1(Евклидова метрика).

Положим .Легко проверить первые два свойства, проверим третье (неравенство треугольника). Нужно доказать, что

.

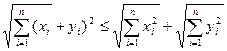
Возведя в квадрат, получим .

Это неравенство верно, если левая часть отрицательна или равна нулю. Если она положительна, рассмотрим квадратный трёхчлен

. В силу последнего неравенства, его дискриминант неположителен, 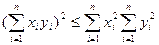,что и требовалось доказать.

2(Кубическая метрика).

Положим . Все свойства легко проверяются.

3(Октаэдрическая метрика). Положим . Опять все свойства проверяются легко.

Любая из этих метрик позволяет определить понятие предела, сходимости, непрерывности, окрестности, предельной точки. В дальнейшем, в зависимости от рассматриваемых задач, будут использоваться первые две метрики. С точки зрения сходимости и непрерывности они приводят к одинаковым результатам, поскольку в любой окрестности с точки зрения метрики 1 содержится окрестность с точки зрения метрики 2 и наоборот.

Операция 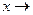называется введением нормы, если она удовлетворяет требованиям(1)-(3).

Расстояние с помощью нормы определяется как (это, собственно, и есть метрика!). Проверяется, что обычные свойства расстояния на плоскости выполняются (проверяются так же, как для нормы).

1. Некоторые подмножества в

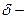окрестностью точки называется множество точек , для которых .Обозначение – старое: .

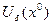Было бы полезно для читающего построить окрестности какой-нибудь точки плоскости в трёх приведённых метриках.

Определение 1.1. Множество называется открытым, если любая его точка принадлежит ему вместе с некоторой своей окрестностью.

Определение 1.2. Точка называется предельной точкой этого множества, если в любой окрестности точки 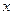содержится бесконечномного точек множества .

Определение 1.3. Множество называется замкнутым, если оно содержит все свои предельные точки.

Множества 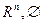одновременно замкнуты и открыты.

Определение 1.4. Множество называется дополнением множества .

Очевидно, .

Теорема 1.1 (о дополнении). Дополнение к открытому множеству замкнуто, дополнение к замкнутому – открыто.

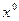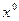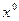Доказательство. 1.Пусть - открытое множество. Нужно доказать, что замкнутое. Пусть - предельная точка множества . Тогда в любой окрестности точки есть элементы множества .Следовательно, не может принадлежать , которое состоит из точек, входящих в него вместе с некоторой окрестностью. Значит, .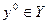

2.Пусть - замкнутое множество. Нужно доказать, что открыто. Если это не так, найдётся точка 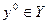, в любой окрестности которой есть элементы из . Но тогда она – предельная для , и, следовательно, должна принадлежать .Противоречие. Теорема доказана.

Теорема 1.2 (о замкнутости и открытости пересечений и объединений множеств). Имеют место следующие утверждения:1)Объединение любого количества (конечного или бесконечного) открытых множеств открыто;2)Объединение конечного числа замкнутых множеств замкнуто;3)Пересечение любого числа замкнутых множеств замкнуто;4)Пересечение конечного числа открытых множеств открыто.

Доказательство. 1) Любая точка объединения принадлежит хотя бы одному из множеств объединения, в которое (они все – открытые!) она входит вместе с некоторой окрестностью; но тогда эта окрестность содержится и в объединении.2) Пусть - сходящаяся последовательность из конечного объединения замкнутых множеств. Тогда у неё есть подпоследовательность, целиком состоящая из элементов одного из этих множеств. Поскольку подпоследовательность сходится к той же точке, а множество замкнуто, 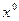должна принадлежать тому же множеству; но тогда она принадлежит и объединению. 3) Предельная точка пересечения замкнутых множеств является предельной для любого из них и, следовательно, принадлежит всем им, т.е., пересечению. 4) Следует из того, что пересечение окрестностей – окрестность. Теорема доказана.

Задача: показать, что если в 2) и 4) отбросить требование конечности числа множеств, утверждения станут неверными.

Теорема 1.3(для особо любопытных) .

Определение 1.5. Непрерывной кривой, соединяющей точки , называется векторная функция , где , и .

Вместо может быть любой отрезок. Определение означает, что при переходе от одной точки к другой координаты меняются непрерывно.

Определение 1.6. Множество называется связным, если любые две его точки можно соединить непрерывной кривой, состоящей из точек множества .

Определение 1.7. Множество называется ограниченным, если его можно поместить в некоторую окрестность одной из его точек(можно определять это понятие и иначе).

Определение 1.8. (Полярные координаты) На плоскости можно ввести систему координат следующим способом. Выберем какую-нибудь точку, , и произвольную полупрямую с началом в этой точке (полярную ось). На полупрямой выберем единичный отрезок. Тогда любой точке плоскости можно сопоставить две координаты: расстояние от до этой точки, , и угол отсчитываемый против часовой стрелки от полупрямой до направления на выбранную точку. Если на той же плоскости введены декартовы координаты, начало которых совпадает с точкой , а ось Ох совпадает с полярной осью и единичные отрезки одинаковы, то имеем: , и . Аналогичную конструкцию можно соорудить для пространства большего числа измерений, но пока она нам не понадобится.

2. Пределы и непрерывность функций

2.1.Определение предела функции ничем не отличается внешне от определения предела для функций одной переменной:

, или аналогичное определение в окрестностях. Поэтому все утверждения, доказанные с использованием свойств модуля, остаются верными и для функций нескольких переменных. Точно так же, остаётся верным утверждение о том, что определение предела по Коши эквивалентно определению предела по Гейне.

Геометрически предел функции при означает, что вся окрестность точки 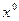стягивается к этой точке. На плоскости можно ввести полярные координаты, для которых начальной точкой будет ; тогда, если полярная ось параллельна оси Ох, а угол отсчитывается от неё до направления на точку , будем иметь , где ; предел функции с точки зрения координат 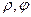- это предел при и , меняющемся произвольно.

Примечание. Есть разница между и ; второй из этих пределов называется повторным; в нём сначала берётся внутренний предел от функции одной переменной , а потом – внешний предел по переменной .Может существовать , а оба повторных(или один из них) не существовать, могут существовать оба повторных, но не существовать общий предел.

Примеры:1. 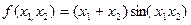; 2. при .

2.2.Определение непрерывной функции ничем не отличается от аналогичного определения для функций одной переменной. Доказательства свойств остаются точно такими же. Пример функции показывает, что функция, непрерывная в точке по каждой из переменных, может не быть непрерывной как функция двух (или большего числа) переменных.

2.3.Теоремы Коши, Вейерштрасса и Кантора.

Теоремы Вейерштрасса, объединённые в одну, для функций многих переменных выглядят так.

Теорема Вейерштрасса. Пусть функция непрерывна на замкнутом ограниченном множестве. Тогда она достигает на этом множестве своих максимума и минимума.

Доказательство может быть получено точно таким же способом, как для одномерного случая (от противного, с использованием аналога леммы о стягивающихся отрезках (леммы о стягивающихся кубах), либо самой этой леммы с помощью проекции на оси координат).

Теорема Коши. Пусть функция непрерывна на связном множестве , пусть . Тогда , такой, что .

Доказательство получается почти автоматически, если соединить точки непрерывной кривой. Вдоль этой кривой функция будет непрерывной функцией одной переменной, для которой теорема Коши уже доказана.

Теорема Кантора. Функция, непрерывная на ограниченном замкнутом множестве, равномерно непрерывна на нём.

Доказательство – такое же, как для функций одной переменной.

3.Дифференцируемость функций нескольких переменных.

Определение 3.1. Функция называется дифференцируемой в точке 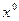, если она определена в некоторой окрестности этой точки, 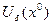, и её приращение в этой точке может быть представлено в ви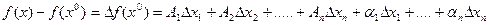де

, где - константы, зависящие только от точки 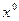, а .

Следствие 3.1. Функция, дифференцируемая в точке, непрерывна в этой точке.

3.2.Частные производные.(Определение 3.2)

Пусть все равны 0. Тогда функция , и

, где - бесконечномалая при . Иными словами, , и - её производная в точке . Эта производная называется частной производной функции в точке 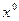по переменной .

Следствие 3.2. Если функция дифференцируема в точке, то все её частные производные в этой точке существуют.

Определение 3.3. Выражение

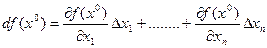для дифференцируемой функции называется дифференциалом этой функцией в точке 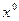или главной (линейной) частью её приращения в этой точке. Вектор называется градиентом функции в точке .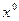

Следствие 3.3.(Необходимое условие локального экстремума) В точке локального экстремума дифференцируемой функции градиент равен нуль-вектору.

Доказательство. Если зафиксировать все координаты, кроме одной, то получится функция одной переменной. Если исходная функция нескольких переменных имеет в точке локальный экстремум, то наша функция одной переменной имеет там локальный экстремум, значит, её производная там должна равняться 0.

Как показывает пример функции , наличие частных производных не является гарантией даже непрерывности. Далее будет приведено достаточное условие дифференцируемости, но сначала разберёмся с разностью . Положим . Тогда для дифференцируемой функции и обратно (т.е., эти записи остаточного члена эквивалентны). В одну сторону доказательство очевидно: , и сумма является бесконечномалой при , так как все дроби не превосходят 1. С другой стороны, если разность между приращением и дифференциалом может быть представлена в виде 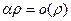, то .

Очевидно, что выражения в скобках стремятся к 0 при .

Теорема 3.3.1. Если частные производные функции в точке 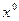непрерывны, то функция в этой точке дифференцируема.

Доказательство. Предположим, что условия теоремы выполнены. Имеем

Теорема доказана.

Можно несколько ослабить условия, потребовав непрерывности всех частных производных, кроме одной. Но вообще условия теоремы не являются необходимыми.

Функция может быть дифференцируемой в точке, не будучи непрерывной ни в какой её окрестности, например , где - функция Дирихле от .

3.4. Производная вдоль вектора или по направлению

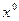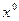Определение 3.4.1. Пусть функция определена в некоторой окрестности точки и пусть - некоторый вектор. Производной вдоль вектора функции и точке называется, если он существует, предел

; если вектор - единичный, получившаяся производная называется производной по направлению.

Теорема 3.4.1. Если функция дифференцируема в точке 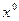, то .

Доказательство. Запишем приращение вдоль вектора

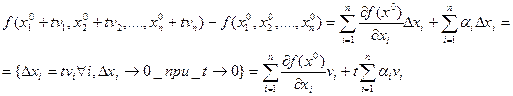
Поделив на и взяв предел при получим доказательство, т.к. все .

3.5.Геометрический смысл дифференцируемости

Как и для случая одной переменной, дифференцируемость функции в точке эквивалентна наличию касательной плоскости (невертикальной) к графику функции в этой точке.

Определение касательной плоскости к графику функции аналогично случаю функции одной переменной.

3.6.Замена переменных и инвариантность формы первого дифференциала

Пусть 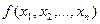определена в некоторой окрестности точки 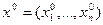, и пусть . Функции 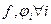предполагаются дифференцируемыми. Мы докажем, что при этих условиях функция 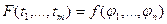будет дифференцируема в точке и получим формулы для вычисления её частных производных.

Имеем

При 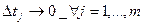обе суммы слева будут , так как .

Следовательно, и форма дифференциала не зависит о того, будут независимыми или нет. Мы доказали инвариантность формы первого дифференциала.

Имеем, далее

. Выражение при - это производная .

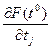Понятно, что инвариантности второго дифференциала и старших дифференциалов не будет (её нет для частного случая – функций одной переменной). Но сначала их надо определить.

3.7. Дифференциалы старших порядков.

3.7.1. Будем считать, что - независимые переменные. Частные производные могут быть дифференцируемыми функциями от , и в этом случае можно определить второй дифференциал . Вообще, если уже определён и является дифференцируемой функцией, то .Для наших целей в основном требуется второй дифференциал.

Если вычислять его непосредственно, получится примерно вот что (ограничимся случаем двух переменных, чтобы формулы выглядели проще).

Два средних члена этой суммы называются смешанными производными. Пример функции

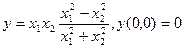показывает, что они могут быть различными. Однако для «хороших» функций значение смешанных производных не зависит от порядка дифференцирования.

Теорема 3.7.1. Пусть функция определена в некоторой окрестности точки и . Пусть смешанные вторые частные производные, существуют и непрерывны в той же окрестности. Тогда .

Доказательство. Рассмотрим дробь

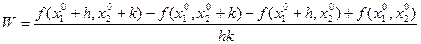, где выбраны так, чтобы точки оставались внутри . Пусть . Тогда

.Функция , по теореме Лагранжа получим .

Преобразуя 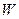другим способом, получим

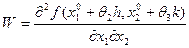.Устремляя к 0 и пользуясь непрерывностью вторых смешанных производных, получим нужное равенство. Теорема доказана.

Другой вариант условий, при которых смешанные производные не зависят от порядка дифференцирования, - потребовать, чтобы 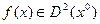. По индукции можно доказать следующий результат: значение смешанных производных любого порядка не зависит от порядка дифференцирования, если эти производные непрерывны в исследуемой точке.

3.7.2. Рассмотрим теперь случай когда .

Имеем

. Есть один случай, когда вторая сумма равна нулю: так будет, если для всех , т.е. если замена линейная. Если она имеет вид , старшие дифференциалы заведомо будут инвариантны при такой замене.

4.Формула Тэйлора

Теорема 4.1. Пусть функция 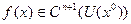. Тогда

Доказательство. Пусть . Тогда точку отрезка можно записать в виде

. На указанном отрезке будет функцией одной переменной, . Для функции

имеет место формула Тэйлора

, где . Далее,

так как - константа. Аналогично, 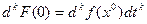, .Вспомним теперь, что нас интересует . В этом случае , и теорема доказана.

5. Достаточное условие локального безусловного экстремума

Теорема 5.1. Пусть 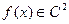и 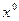- точка, в которой выполнено необходимое условие локального экстремума. Тогда, если , в точке минимум, если , в точке максимум, если второй дифференциал меняет знак, то в точке нет экстремума; если второй дифференциал полуопределён, требуется дополнительное исследование.

Доказательство. Формула Тэйлора в стационарной точке выглядит так

Доказательство. Разберём один случай, так как все они исследуются одинаково, кроме последнего, в котором существенно поведение . Пусть

, где коэффициенты – вторые производные в точке .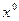

Сумма, на которую умножается , определена на единичной сфере и по теореме Вейерштрасса достигает там максимума и минимума. Если она положительно определена, то минимум не может быть отрицательным или равным нулю. В этом случае поведение несущественно. Тот же вывод имеет место, если она отрицательно определена или меняет знак.

Если же квадратичная форма полуопределена, то можно привести разнообразные примеры (как в случае функций одной переменной при равном нулю втором дифференциале). Теорема доказана.

Дата добавления: 2015-08-26