Определённый интеграл

1. Мы будем рассматривать функции, определённые на отрезке . Разбиением отрезка называется выбор точек 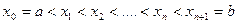.(Неравенства могут быть в другую сторону, но все сразу). Мелкостью разбиения называется 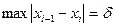. Интегральной суммой для данного разбиения называется сумма вида

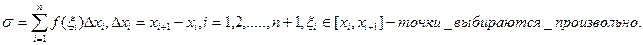
Определение 2.1. Определённым интегралом 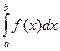называется, если он существует, 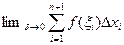.Если определённый интеграл существует, функция называется интегрируемой по Риману на отрезке .

Отметим, что в определении не говорится ничего о выборе точек 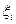; их можно выбирать любым способам, лишь бы 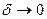. То есть, никакие конкретные суммы при взятии предела не рассматриваются, ибо при любом фиксированном 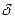таких сумм бесконечно много. Тем не менее, рассмотрение интегральных сумм иногда полезно.

Следствие 1.1. Функция 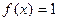интегрируема, и .

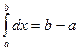Действительно, для любого разбиения и любого выбора точек 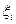интегральная сумма равна .

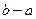Теорема 2.1. Если функция интегрируема на отрезке то она на нём ограничена.

Доказательство. Предположим, что не ограничена в точке 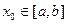.При любом 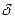, можно выбирать точки 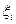так, чтобы: 1)произведение 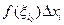для отрезка 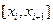, на котором лежит точка 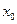, было сколь угодно большим по модулю; 2) чтобы остающаяся часть интегральной суммы была по модулю меньше половины модуля указанного произведения. Если функция интегрируема, у таких интегральных сумм должен быть конечный предел, что противоречит принципу их построения. Теорема доказана.

В дальнейшем мы будем рассматривать только ограниченные на отрезке функции.

Теорема 2.2. Если функция на отрезке 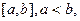интегрируема и не отрицательна, то интеграл от неё не меньше нуля.

Доказательство. Любая интегральная сумма будет неотрицательной, значит и предел этих сумм неотрицателен.

Теорема 2.3. Если на отрезке 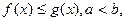и обе функции интегрируемы, то

.

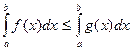Очевидное следствие из предыдущего утверждения.(Применить предыдущую теорему к )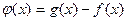

Теорема 2.4. Множество 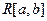интегрируемых на отрезке функций образует линейное пространство.

Достаточно сравнить интегральные суммы.

Теорема 2.5. .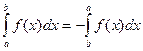

Очевидно из определения интегральной суммы.

Теорема 2.6. Если 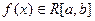, то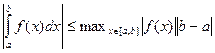

Доказательство – из свойств модуля и интегральных сумм

С точки зрения Теорем 2.5,2.6, естественно положить по определению

,

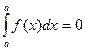если на некотором отрезке функция интегрируема.

Суммы Дарбу.

Будем для удобства считать, что .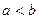

Определение 2.2. Пусть есть некоторое разбиение отрезка . Пусть 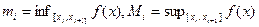; положим

.

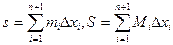Эти суммы называются нижней и верхней суммами Дарбу. В наших предположениях, всегда 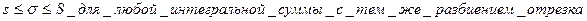. Суммы Дарбу зависят только от разбиения отрезка и не зависят от выбора точек .

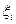Теорема 2.7. При добавлении к данному разбиению одной точки нижняя сумма может только увеличиться, верхняя – только уменьшиться.

Доказательство. Пусть 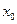- новая точка разбиения, и пусть она лежит на отрезке разбиения 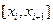. Ни на одном из вновь образовавшихся отрезков нижняя грань функции не может стать меньше, а верхняя – не может стать больше, чем на исходном отрезке. Теорема доказана.

Теорема 2.8. Для любых двух разбиений нижняя сумма первого (второго) не может превосходить верхнюю сумму второго(первого).

Доказательство. Рассмотрим третье разбиение, которое получается, если объединить точки первого и второго разбиений. Нижняя сумма для третьего будет не меньше, чем для первого, верхняя для третьего будет не меньше, чем нижняя для третьего и не больше, чем верхняя для второго, согласно предыдущей теореме. Теорема доказана.

Теорема 2.9. Существуют

.

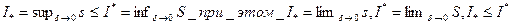Доказательство. По предыдущей теореме, множество нижних сумм ограничено сверху, а множество верхних сумм – снизу. Значит, у этих множеств есть, соответственно, верхняя и нижняя грани. Взятие пределов предполагает добавление точек разбиения, при котором нижние суммы не убывают, верхние не возрастают. Значит, предел нижних сумм будет существовать и совпадать с верхней гранью, а для верхних сумм – совпадать с нижней гранью. Неравенство из условия теоремы получится, если перейти к пределу в неравенстве 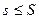. Теорема доказана.

Теорема 2.10. (Критерий интегрируемости) Для того, чтобы функция была интегрируема на отрезке , необходимо и достаточно, чтобы .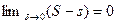

Доказательство. Достаточность. Если условие теоремы выполнено, то 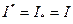.Для любого 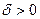, и для любого выбора точек 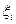имеет место неравенство 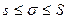. Следовательно, предел интегральных сумм существует и равен .

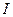Необходимость. Если интеграл существует, то 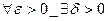, такое, что для всех интегральных сумм с мелкостью меньше 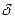будет выполняться система неравенств 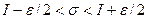.Перейдём сначала в левом неравенстве к верхней грани, потом в правом – к нижней. Получим 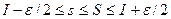; то есть, разница 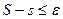. Поскольку 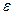произвольно, теорема доказана.

Определение 2.3. 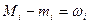называется колебанием функции на отрезке .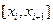

Критерий интегрируемости функции на отрезке эквивалентен требованию

.

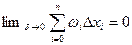Дата добавления: 2015-08-26