Теорема о неявной функции

Теорема о неявной функции является одной из важнейших теорем математического анализа. Она рассматривает задачу о разрешимости уравнения f(x,y)=0 относительно y; в разных её вариантах x,f,y могут быть скалярами или векторами. Следствия из неё широко используются, в частности, в теории условного экстремума и в экономических приложениях. Далее эта теорема, вместе с некоторыми приложениями, будет изложена в различных вариантах.

1.Рассмотрим функцию u = f (x,y), имеющую непрерывные частные производные в некоторой окрестности U(a,b) точки (a,b).

Теорема 1. Пусть производная по y функции f (x,y) в точке (a,b) отлична от 0, f(a,b)=0.

Тогда найдётся окрестность U₀(a,b), в которой y можно представить как функцию от x, y=w(x), такую, что b=w(a), w является дифференцируемой функцией от x, и w ′= - f ′_x/f ′_y.

Доказательство. Для определённости, пусть производная по y в точке a положительна. Тогда функция f(a,y) монотонно возрастает в точке b и, значит, для y>b f (a,y)>0, а для y<b f(a,y)<0. Рассмотрим теперь две функции, f(x,b-e) и f(x,b+e), выбрав e так, чтобы мы не вышли за U(a,b). Поскольку f(x,y) имеет непрерывные частные производные в U(a,b), она там дифференцируема и, значит, непрерывна; следовательно, функции f(x,b-e), f(x,b+e) непрерывны в некоторой общей для них окрестности точки a, (a-s,a+s). Согласно лемме об устойчивости знака, s можно выбрать так, чтобы во всей этой окрестности выполнялись неравенства f(x,b-e)<0, f(b+e)>0.

Рассмотрим теперь окрестность (a - s,a + s). Для всякого x из этой окрестности функция F(y)=f(x,y) монотонно возрастает как функция от y и непрерывна; по теореме Коши о промежуточном значении, найдётся точка y из (b-e,b+e), в которой F(y)=0, и в силу монотонности F такая точка только одна. Мы доказали, что в окрестности V(a,b) для всякого x из (a-s,a+s) найдётся единственный y из (b-e,b+e), для которого f(x,y)=0. Положим y=w(x). Тогда f(x,w(x))=0 по определению w(x) для всех x из (a-s,a+s).

Докажем теперь, что w(x) непрерывна в (a-s,a+s). Для точки a непрерывность очевидна: мы по e выбрали s, такое, что как только x попадает в s-окрестность точки a, y попадает в е - окрестность точки b, Если взять любую другую точку (x₁,y₁), x₁ из (a‑s,a+s), y₁ из (b-e,b+e), такую, что f(x₁,y₁)=0, то для неё будут выполнены те же условия, что для (a,b). Значит, у неё найдётся окрестность, в которой y=w₁(x) и w₁ непрерывна в x₁. Но w₁(x)=w(x), так как условие f(x,w(x))=0 однозначно определяет функцию w(x).Следовательно, y=w(x) непрерывна для всех x из (a-s,a+s).

Докажем, что w(x) дифференцируема.

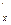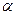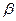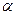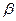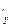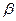
Как было отмечено выше, f(x,y) дифференцируема в U(a,b). Рассмотрим приращение f(x,w(x))-f(a,b)=0=f (a,b)*(x-a)+f′_y(a,b)*(w(x)-b) + *(x – a) + *(w(x) –b), где и бесконечно-малые. Выберем такую окрестность точки (a,b) чтобы f + 0. Это можно сделать, потому что 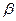бесконечно малая. Эта окрестность и есть U (a,b). Имеем

=

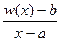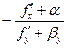
При x стремящемся к a w(x) стремится к b, 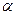и 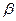- к 0. Получаем

w = -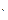

Если рассмотреть другую точку из U (a,b), то, рассуждая как при доказательстве непрерывности w(x), получим, что w(x) дифференцируема для всех (x,w(x)) из V (a,b).

Теорема доказана.

Примечания. 1. Для доказательства существования w(x) достаточно потребовать непрерывность f(x,y) и её монотонность по y.

2.Требование неравенства 0 производной по y (или по x) не является необходимым. Уравнение (y-x) 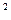=0 однозначно разрешимо, хотя обе частные производные равны 0.

2. Теорема 2. Пусть функция u=f(x₁,x₂,…..,x_n,y) =f(x,y) определена и непрерывна вместе со своими частными производными в некоторой окрестности U(x₀,y₀) точки (x₀,y₀), причём f(x₀,y₀)=0, и имеет ненулевую частную производную по y в самой точке (x₀,y₀). Тогда существует окрестность U (x₀,y₀), в которой y=w(x)=w(x₁,x₂,…..,x_n), функция w(x) непрерывна вместе со своими частными производными в окрестности U₀, w(x₀)=y₀ и

= -

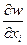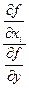
Доказательство этой теоремы совершенно аналогично доказательству Теоремы 1.

Следствие 1. (Уравнение касательной к неявной функции) Пусть выполнены условия Теоремы 2. Тогда уравнение касательной к функции y=w(x) в точке (x₀,y₀) может быть записано в виде

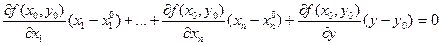
Действительно, уравнение касательной к y=w(x) в указанной

точке имеет вид

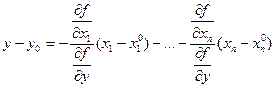
Умножив его на 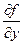и перенеся всё в левую часть, получим, что требовалось доказать. Легко получить тот же результат из геометрических соображений. Действительно, если уравнение касательной к графику функции u=f(x,y) в точке (x₀,y₀) имеет вид

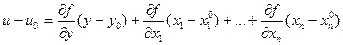
то при сечении графика плоскостью u=u из графика высекается множество уровня, а из касательной плоскости к графику – касательная к множеству уровня.

Следствие 2. Пусть в условиях Теоремы 2 рассматривается уравнение f(x,y)=c,где c – некоторая константа, и f(x₀,y₀)=c. Рассмотрев функцию u =f(x,y)-c, мы увидим, что она удовлетворяет условиям Теоремы 2. По Следствию 1, получим касательную к соответствующей неявной функции в виде

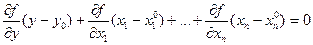
С другой стороны, уравнение f(x,y)=c представляет множество уровня функции f. Теорема 2 показывает, что множество уровня является некоторой поверхностью, касательная к неявной функции w(x) в точке (x₀,y₀) – касательной к этой поверхности, а уравнение касательной, которое мы получили, - что градиент функции f в точке (x₀,y₀) ортогонален поверхности уровня функции f.

Формулировка Следствия 2. Пусть функция u=f(x,y) определена в некоторой окрестности точки (x₀,y₀), пусть её частные производные непрерывны в этой точке, производная по y в этой точке отлична от нуля и f(x₀,y₀)=c. Тогда в некоторой окрестности точки (x₀,y₀) множество уровня f=c является поверхностью, и градиент функции f ортогонален этой поверхности уровня в точке (x₀,y₀).

3. Теорема 3 (о векторной неявной функции). Пусть функции f₁(x₁,x₂,….,x_n,x_n+1,…x_n+m), …..,f_m(x₁,x₂,….,x_n,x_n+1,…x_n+m) непрерывно дифференцируемы в некоторой окрестности U(x₀) точки x₀, пусть

f₁(x₀)=0,f₂(x₀)=0,….,f_m(x₀)=0,

и пусть определитель J(x₀),

отличен от нуля. Тогда найдётся окрестность U(x₀) точки x₀, в которой

x_n+1=w₁(x₁,x₂,….,x_n),…,x_n+m= w_m(x₁,x₂,….,x_n), причём функции w₁,…,w_m

непрерывно дифференцируемы и

f₁(x₁,…,x_n,w₁,…,w_m)=0,…,f_m(x₁,…,x_n,w₁,…,w_m)=0.

Теорема утверждает, что, если выполнены её условия, последние координаты точки 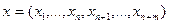в некоторой окрестности точки 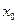можно выразить как непрерывно-дифференцируемые функции первых.

Доказательство (индукция по числу уравнений).

Если m=1, то мы находимся в условиях Теоремы 2, и всё доказано.

Пусть m>1. Предположим, что теорема уже доказана для всех k<m, в частности, для k=m-1. Рассмотрим последнее уравнение. Поскольку J(x₀)=/=0, и поскольку частные производные, из которых он составлен, непрерывны, по лемме об устойчивости знака найдётся окрестность точки 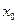, U₁(x₀), в которой он будет всё ещё отличным от нуля. В этой окрестности хотя бы один из элементов его последней строки будет отличен от нуля. Пусть, для определённости, это будет её последний элемент, . Тогда, по Теореме 2, найдётся окрестность U₂(x₀), в которой x_n+m можно будет выразить в виде функции w₀(x₁,…,x_n+m-1). В окрестности U₂(x₀) система уравнений, данная в условиях Теоремы 3, будет эквивалентна системе

……………………

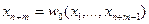
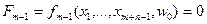Рассмотрим теперь систему из последних 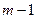уравнений. Если мы докажем, что в некоторой окрестности точки x₀ определитель

не равен нулю, то, используя предположение индукции, мы выразим x_n+1,…,x_n+m-1 как функции от x₁,…,x_n, которые будут непрерывно-дифференцируемыми. Подставив эти функции в w₀, получим выражение для x_n+m в виде непрерывно-дифференцируемой функции от x₁,…,x_n, и Теорема 3 будет доказана.

Докажем, что 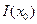отличен от нуля. Для этого в определителе J к 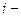тому, 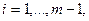столбцу прибавим последний, умноженный на 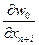; получим

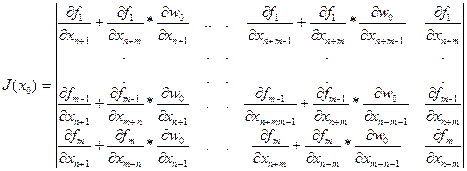
Определитель размерности (m-1), стоящий в левом верхнем углу, есть просто 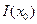В нижней строке

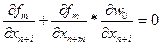
Получаем

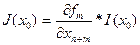
Значит, 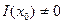, и Теорема 3 доказана.

Примечания. 1. Теорема 3 не утверждает, что, при отличном от нуля якобиане на всей области определения функций f₁,…,f_m, последние координаты однозначно во всей области определяются по первым. Для системы

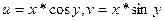
якобиан всюду отличен от нуля при 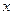>0 (он равен x), но однозначной разрешимости относительно u и v не будет.

2.Легко сообразить, что Теорема 3 утверждает следующее. Если градиенты функций f₁,…,f_m линейно-независимы в точке x₀, то в некоторой окрестности точки x₀ m её координат можно рассматривать как функции от остальных.

Теория локального условного экстремума

В этом разделе будет рассматриваться следующая задача:

Найти экстремумы функции u=f(x)=f(x₁,…,x_n) при условиях f₁(x)=0,….,f_m(x)=0, m<n; все функции предполагаются непрерывными вместе с первыми или, по потребности, со вторыми частными производными, а градиенты функций f₁,….,f_m – линейно-независимыми. Мы будем, кроме того, предполагать, что все рассматриваемые точки содержатся в области определения функции f(x) вместе с некоторой окрестностью (открытой) и что пересечение этой окрестности с множеством точек, удовлетворяющих условиям f₁(x)=0,…,f_m(x)=0 не пусто. Сами условия обычно называются уравнениями связей.

Точка x₀,удовлетворяющая уравнениям связей, называется точкой локального условного экстремума функции f(x), если значение f(x₀) является самым большим или самым маленьким среди значений f(x) для точек x, удовлетворяющих уравнениям связей (соответственно, получается локальный условный максимум или локальный условный минимум).

Необходимое условие локального условного экстремума.

1). Разберёмся сначала с геометрией. Пусть x₀ удовлетворяет системе уравнений f₁=0,…,f_m=0. Множество векторов 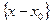, касательных в точке x к гладкой поверхности H(x₀), которую, согласно Теореме 3, порождают точки, удовлетворяющие этой системе, является множеством решений системы

……………….

,

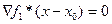
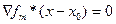где 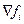- градиенты к поверхностям, высекаемым из общей области допустимых x-ов отдельными ограничениями. Это множество называется касательным многообразием L(x₀) в точке x₀ к поверхности H(x₀). Если градиент функции f в точке x₀ имеет ненулевую проекцию на L(x₀), то на L(x₀) есть направление, в котором функция f возрастает, и, значит, на H(x₀) есть точки x, в которых значение f(x)>f(x₀), и, точно так же, есть точки x, в которых значение f(x)<f(x₀). В этом случае точка x₀ не может быть точкой локального условного экстремума. Значит, необходимым условием того, чтобы точка x₀ была точкой локального условного экстремума, является равенство нулю проекции градиента на L(x₀), что означает, что сам градиент функции f в точке x₀ лежит в ортогональном дополнении к L(x₀). В свою очередь, ортогональное дополнение к L(x₀) порождается градиентами ограничений, взятыми в точке x₀, которые у нас, по условию, линейно-независимы. Мы получили следующее необходимое условие: точка x₀ может быть точкой локального условного экстремума функции f при условиях f₁=0,…,f_m=0 только в том случае, если градиент функции f в точке x₀ есть линейная комбинация градиентов ограничений, то есть

…..+ *

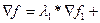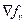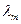
2). То же самое условие можно получить иначе. Рассмотрим функцию

La(x₁,x₂,…,x_n;y₁,…,y_m) = f +(y₁)*f₁ + (y₂)*f₂ + …+ (y_m)* f_m.

Ясно,что при любых y,при условиях

f =0,….,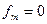

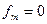
экстремумы функций f и La совпадают. Подберём y так, чтобы условный экстремум функции f совпадал с безусловным экстремумом функции La. Приравняем нулю частные производные функции Лагранжа. Получим

………………………………………..

……………….

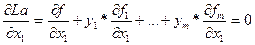
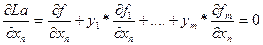
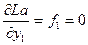
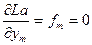
Пусть x - точка условного экстремума функции f при заданных условиях. Частные производные функции Лагранжа по переменным y задают ровно эти самые условия. Рассмотрим теперь систему уравнений

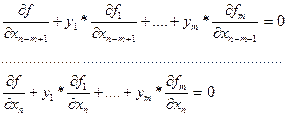
в точке x . В этой точке определитель, стоящий при переменных y, отличен от нуля по предположению о линейной независимости градиентов ограничений.. Следовательно, можно найти 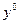, являющиеся решением данной системы. Рассматривая далее функцию Лагранжа с коэффициентами 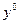, мы видим, что её дифференциал будет равен нулю в том, и только в том случае, если будет выполняться система уравнений

так как независимы. Следовательно, с одной стороны, мы получаем, что градиент функции f является линейной комбинацией градиентов ограничений,а с другой стороны, что точки локального условного экстремума

функции f можно искать как точки обычного локального экстремума функции Лагранжа, что и требовалось.

Теорема 4. Для того, чтобы точка 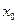была точкой локального условного экстремума, необходимо, чтобы градиент целевой функции был линейной комбинацией градиентов ограничений.

Достаточные условия локального условного экстремума.

Пусть 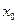– точка, подозреваемая на условный локальный экстремум, 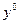– соответствующие множители Лагранжа. Как уже отмечалось, при условиях

экстремумы функций f и La совпадают, равно как и значения в точках, удовлетворяющих условиям. Значит, исследование на наличие экстремума можно проводить с помощью функции Лагранжа. Рассмотрим приращение функции Лагранжа в точке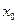

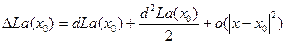
В этом выражении первый дифференциал равен нулю согласно выбору коэффициентов y . А во втором дифференциале зависимые 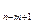dx ,…,dx 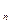можно исключить, продифференцировав уравнения связи. Наконец, можно заменить дифференциалы на приращения соответствующих переменных, до исключения зависимых дифференциалов или после – это вызовет изменение только в 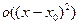. Знак приращения функции Лагранжа будет совпадать со знаком второго дифференциала после проведённой замены. Если второй дифференциал окажется положительно-определённым, то в точке x – минимум; если отрицательно-определённым,- то максимум; если второй дифференциал меняет знак, то в точке нет локального условного экстремума; во всех остальных случаях требуется дополнительное исследование.

Теорема о маргинальных значениях.

Рассмотрим следующую ситуацию. Пусть x (c) – точка экстремума функции f при

условиях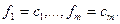

Определим функцию F(c)=f(x (c)). Мы будем предполагать, что для системы условий выполнены требования теоремы 3 о неявной функции в точке 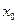. То, что в правых частях условий стоят не нули, не меняет утверждения этой теоремы, только выражения для зависимых x-ов через независимые будут включать вектор c. Предположим для определённости, что точка x (c) – точка строгого локального условного максимума. При малом изменении c x (c) будет дифференцируемой функцией от c и будет оставаться точкой максимума. Пусть y (c) – вектор множителей Лагранжа для точки x (c).

Рассмотрим теперь дифференциал функции F(c) в точке c . Имеем

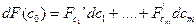
С другой стороны,

…………………………..

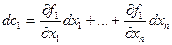
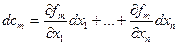
С точки зрения функции Лагранжа

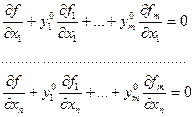
Значит

Следовательно,

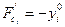
Мы получили Теорему о маргинальных значениях:

Теорема 5. Пусть 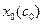- точка строгого локального экстремума функции f(x) при условиях

, причём выполнены условия теоремы 3. Тогда найдётся окрестность точки 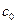, в которой функция 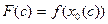, где 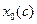- точка экстремума, и сама точка 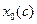являются непрерывно-дифференцируемыми функциями, и

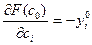
Теорема показывает, как меняется точка экстремума и значение целевой функции с изменением .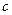

СОДЕРЖАНИЕ

1-ый семестр

Введение

1.Кое-что о множествах

2.Теория последовательностей

2.1. Сходящиеся последовательности

2.2. Последовательности, не имеющие предела

3. Предел функции

3.1 – 3.2. Предел функции в точке, определения предела по Гейне и Коши. Критерий Коши

3.3. Нечто об эквивалентности и о-малых

4. Непрерывность

4.1 – 4.2. Непрерывность функции в точке; непрерывность сложной функции

4.3. Свойства функций, непрерывных на отрезке

5. Дифференцируемость функции

6. Теоремы о дифференцируемых функциях

7. Выпуклые функции

8. Дополнительные сведения о дифференцируемых функциях (теоремы Дарбу и теорема о разрывах производных).

2-ой семестр

Интегралы

1 Неопределённый интеграл и первообразная

2. Определённый интеграл.

2.1.-2.6. Свойства, вытекающие непосредственно из определения

2.7 – 2.10. Суммы Дарбу и критерий интегрируемости.

3. Классы интегрируемых функций

4. Интеграл как функция верхнего предела

5. Несобственные интегралы

6. Признаки сходимости

Функции нескольких переменных

Введение

1. Некоторые множества в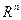

2. Пределы и непрерывность функций нескольких переменных

3. Дифференцируемость функций нескольких переменных

4. Формула Тэйлора

5. Достаточное условие локального безусловного экстремума

Теоремы о неявных функциях

1. Теоремы существования (1 – 4)

2. Необходимое условие локального условного экстремума

3. Достаточное условие локального условного экстремума

4. Теорема о маргинальных значениях

Дата добавления: 2015-08-26