
Читайте также:
|
1. Вычислить интеграл  .
.
2. Вычислить интеграл 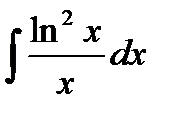 .
.
3. Найти интегралы  .
.
4. Вычислить интеграл  .
.
5. Найти интеграл  .
.
6. Вычислить интеграл 
7. Вычислить интеграл 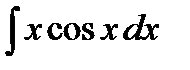 .
.
8. Вычислить интеграл  .
.
9. Вычислить интеграл  .
.
10. Вычислить интеграл 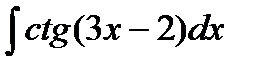 .
.
11. 
12. Вычислить интеграл 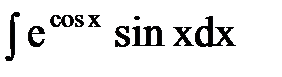 :
:
13. Вычислить интеграл  :
:
14. Вычислить интеграл 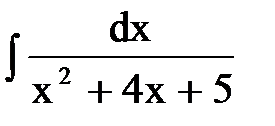 :
:
15. Вычислить интеграл  :
:
16. Вычислить интеграл  :
:
17. Вычислить интеграл  :
:
18. Вычислить интеграл  :
:
Экзаменационные вопросы
1. Числовая последовательность. Монотонная, ограниченная, сходящаяся. Бесконечно большая. Бесконечно малая.
2. Свойства сходящихся последовательностей. Свойства бесконечно малых последовательностей. Связь между бесконечно большими и бесконечно малыми величинами.
3. Теорема Вейерштрасса о существовании предела.
4. Функция и методы ее задания. Классификация функций.
5. Односторонние пределы. Замечательные пределы.
6. Непрерывность функции в точке и на отрезке. Точки разрыва и их классификация.
7. Производная и дифференциал функции. Производная основных элементарных функции. Геометрический и физический смысл производной. Уравнение касательной и нормали.
8. Дифференцируемость функции. Основные правила дифференцирования. Производная сложной, обратной, неявной функции.
9. Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).
Исследование функции. Определение локальных и глобальных экстремумов функции. Необходимое и достаточное условия существования локальных экстремумов.
Направление выпуклости графика функции. Точки перегиба и асимптоты. Необходимое и достаточное условие существования точки перегиба графика функции.
10. Первообразная и неопределенный интеграл, его основные свойства.
11. Таблица основных интегралов и основные методы интегрирования.
12. Теорема Вейерштрасса о непрерывных функциях.
1. Вычислить предел  : А) e2; В) e; С)2; Д) e1/2; Е)1.
: А) e2; В) e; С)2; Д) e1/2; Е)1.
2. Вычислить предел  : А)
: А)  ; В)3; С)
; В)3; С)  ; Д)
; Д)  ; Е)1.
; Е)1.
3. Найти предел функции  : А)1/4; В)1/2; С)0; Д)1; Е)4
: А)1/4; В)1/2; С)0; Д)1; Е)4
4. Найти предел функции  : А) 25/2; В)5/2; С)5; Д)2; Е)7
: А) 25/2; В)5/2; С)5; Д)2; Е)7
5. Найти предел функции  : А)2; В)4; С)3; Д)1; Е)5/2
: А)2; В)4; С)3; Д)1; Е)5/2
6. Найти предел 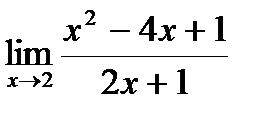 : А) -0.6; В)4; С)6; Д)-1; Е)0.6;
: А) -0.6; В)4; С)6; Д)-1; Е)0.6;
7. Найти предел  : А)
: А)  ; В)2; С)3; Д)1; Е)
; В)2; С)3; Д)1; Е) 
8. Найти предел  : А)
: А) 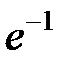 ; В)
; В)  ; С)0; Д)1; Е)
; С)0; Д)1; Е) 
9. Найти предел  : А)
: А)  ; В)
; В)  ; С)1; Д)0; Е)
; С)1; Д)0; Е) 
10. Найти предел  : А)-1; В)0; С)2; Д)
: А)-1; В)0; С)2; Д)  ; Е)1
; Е)1
11. Вычислить предел  А)3; В)1; С)0; Д)
А)3; В)1; С)0; Д)  ; Е)4
; Е)4
**************************************************************************
1. Найти точки разрыва функции  А)
А)  ; В)
; В) 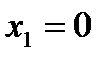 ,
,  ;
;
С) 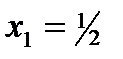 ,
,  ; Д)
; Д) 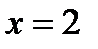 ; Е) функция непрерывна
; Е) функция непрерывна
2. Найти точки разрыва функции 
А)  ,
,  ; В)
; В) 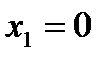 ,
,  ; С) функция непрерывна; Д)
; С) функция непрерывна; Д) 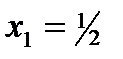 ,
,  ;
;
Е) 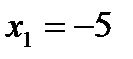 ,
, 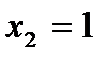
3. Найти точки разрыва функции 
А) функция непрерывна; В)  ; С)
; С)  ; Д)
; Д) 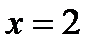 ; Е)
; Е)  ,
, 
4. Найти точки разрыва функции 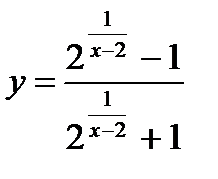
А) 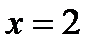 ; В)
; В) 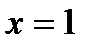 ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
5. Указать точку разрыва, установить их характер 
А)  точка разрыва 1 рода; В)
точка разрыва 1 рода; В) 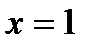 точка разрыва 1 рода; С)
точка разрыва 1 рода; С)  точка разрыва 2 рода;
точка разрыва 2 рода;
Д)  устранимая точка разрыва; Е) непрерывная функция
устранимая точка разрыва; Е) непрерывная функция
6. Указать точку разрыва, установить их характер 
А)  точка разрыва 1 рода; В)
точка разрыва 1 рода; В) 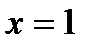 точка разрыва 1 рода; С)
точка разрыва 1 рода; С)  точка разрыва 2 рода;
точка разрыва 2 рода;
Д)  устранимая точка разрыва; Е) непрерывная функция
устранимая точка разрыва; Е) непрерывная функция
7. Указать точку разрыва, установить их характер 
А)  точка разрыва 1 рода; В)
точка разрыва 1 рода; В) 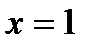 точка разрыва 1 рода; С)
точка разрыва 1 рода; С)  точка разрыва 2 рода;
точка разрыва 2 рода;
Д)  устранимая точка разрыва; Е) непрерывная функция
устранимая точка разрыва; Е) непрерывная функция
8. Указать точку разрыва, установить их характер 
А)  точка разрыва 1 рода; В)
точка разрыва 1 рода; В) 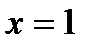 точка разрыва 1 рода; С)
точка разрыва 1 рода; С)  точка разрыва 2 рода;
точка разрыва 2 рода;
Д)  устранимая точка разрыва; Е) непрерывная функция
устранимая точка разрыва; Е) непрерывная функция
**************************************************************
1. Вычислить  , если
, если 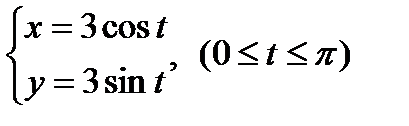
А)-1; В)0; С)1; Д)2; Е)-2
2. Вычислить производную функции  :
:
А)  ; В)
; В)  ; С)
; С) 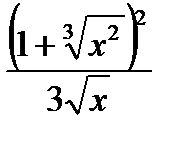 ; Д)
; Д)  ; Е)
; Е) 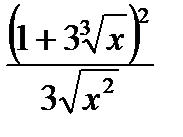
3. Найти производную функции 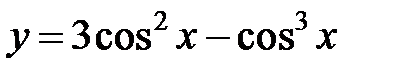 :
:
А)  ; В)
; В)  ; С)
; С)  ;
;
Д)  ; Е)
; Е) 
4. Найти скорость равномерно ускоренного движения 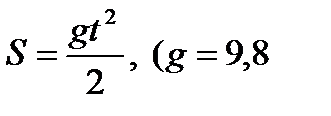 м/сек) в момент времени t=2 сек.
м/сек) в момент времени t=2 сек.
А)19,6; В)9,8; С) 98; Д)3; Е)0
5. Найти значения тангенса угла наклона касательной к кривой 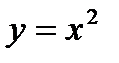 в точке
в точке 
А)-2; В)0; С)1; Д)2; Е)-1
6. Найти производную функции  :
:
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
7. Найти производную функции  :
:
А)  ; В)
; В) 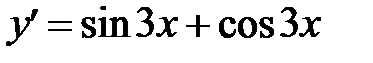 ; С)
; С)  ;
;
Д) 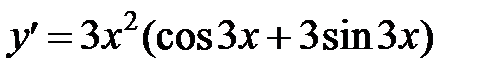 ; Е)
; Е) 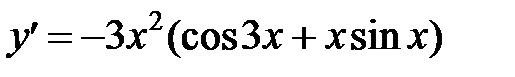
8. Найти производную функции: 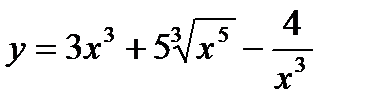 :
:
А)  ; В)
; В) 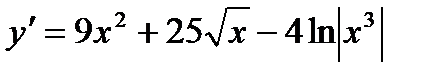 ; С)
; С) 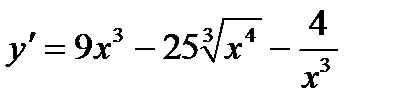 ;
;
Д)  ; Е)
; Е) 
9. Если  , найти
, найти  : А)
: А)  ; В)0,2; С)-0,2; Д)-2; Е)2
; В)0,2; С)-0,2; Д)-2; Е)2
10.  :
:
А)  ; В)
; В)  ; С)-
; С)-  ; Д)
; Д)  ; Е)0
; Е)0
11. Найти  , если
, если 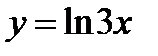
А)-  ; В)
; В) 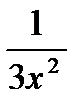 ; С)
; С)  ; Д)3lnx; Е)-
; Д)3lnx; Е)- 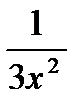
12. Найти  из уравнения
из уравнения 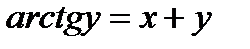 :
:
А)  ; В)
; В)  ; С)
; С) 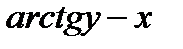 ; Д)
; Д)  ; Е)
; Е) 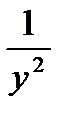
13. Найти  , если
, если  :
:
А) 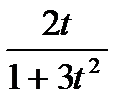 ; В)
; В) 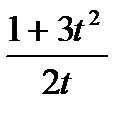 ; С)
; С)  ; Д)1+3t2; Е)
; Д)1+3t2; Е) 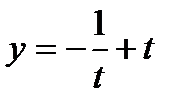
14. Какое равенство является формулой Лагранжа функции  на отрезке
на отрезке  ?
?
А)  , где
, где  ; В)
; В)  ;
;
С)  , где
, где  ; Д)
; Д)  , где
, где  ;
;
Е)  , где
, где 
15. Найти производную функции  , заданной неявно
, заданной неявно 
А)  ; В)
; В)  ; С)
; С) 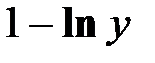 ; Д)
; Д) 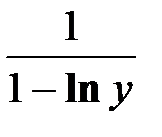 ; Е)
; Е) 
16. Найти 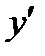
 , если
, если  : А)
: А)  ; В)
; В)  ; С)2; Д)-2; Е)5
; С)2; Д)-2; Е)5
?*****************************************************************
1. Какая из следующих точек для функции  является точкой перегиба:
является точкой перегиба:  ,
, 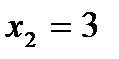 ,
, 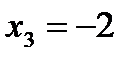 ,
,  ,
, 
А) Никакая; В)  ,
, 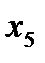 ; С)
; С)  ,
,  ; Д)
; Д)  ,
,  ; Е)
; Е) 
2. Найдите наименьшее значение функции  на отрезке x Î
на отрезке x Î 
А)-15; В)1; С)-31; Д)-6; Е)-25.
3. В каких точках функция  имеет экстремум?:
имеет экстремум?:
А)-2; 2; В)  ; С)2; Д)0; 12; Е)0; 2.
; С)2; Д)0; 12; Е)0; 2.
4. Определить точки максимума функции 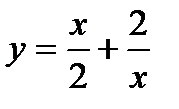 :
:
А)-2; В)2; С)1; Д)2; -2; Е)0; 2.
5. Найти промежутки возрастания функции 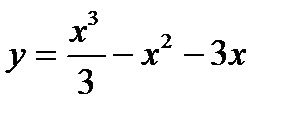 :
:
А)  ; В)
; В)  ; С)
; С) 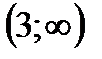 ; Д)
; Д) 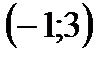 ; Е)
; Е) 
6. Найти точку, в которой будет выполняться теорема Лагранжа для функции  на отрезке
на отрезке 
А)2; В)1; С)4/3; Д)1/3; Е)1/2
7. Найти экстремумы функций 
А)  ; В)
; В)  ; С) экстремума нет; Д)
; С) экстремума нет; Д)  ;
;
Е) 
8. Найти точки минимума функции 
А) 1; В)0; С)2; Д)-1; Е)-2
9. Найти точки максимума функции 
А) -1; В)0; С)4; Д)1; Е)-2
10. Прямая 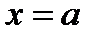 является вертикальной асимптотой, если
является вертикальной асимптотой, если
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
11. Найти точки минимума функции 
А) 3; В)0; С)2; Д)-1; Е)4
12. Сколько точек экстремума имеет функция  на интервале
на интервале  ?
?
А) Одну; В) Ни одной; С) Четыре; Д) Две; Е) Две
13. Найти наклонную асимптоту кривой  :
:
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
14. Найти интеграл 
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
15. 
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
16. Найти интеграл 
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
17. Вычислить интеграл 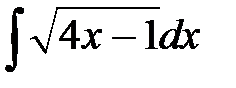 :
:
А)  ; В)
; В)  +C; С)
+C; С)  + C.; Д)
+ C.; Д)  ; Е)
; Е) 
18. Вычислить интеграл  :
:
А)-  + C; В)
+ C; В) 
 + C; С)
+ C; С) 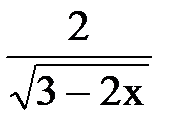 + C; Д)-2
+ C; Д)-2 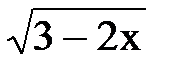 + C; Е)2
+ C; Е)2 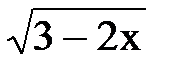 + C.
+ C.
19. Вычислить интеграл  :
:
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
20. Вычислить интеграл  :
:
А)-  ; В)
; В)  ; С)
; С) 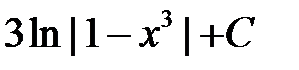 ; Д)
; Д)  ; Е)
; Е) 
21. Вычислить интеграл 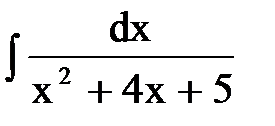 :
:
А)  ; В)
; В) 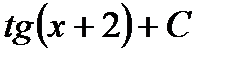 ; С)
; С) 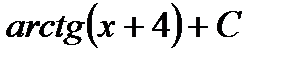 ; Д)
; Д)  ; Е)
; Е) 
22. Вычислить интеграл  :
:
А)  ; В)
; В) 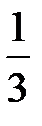 arctgx + C; С)
arctgx + C; С)  arcctg
arcctg 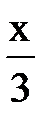 + C; Д)
+ C; Д)  + C; Е)
+ C; Е)  + C
+ C
23. Вычислить интеграл  :
:
А)  ; В)
; В) 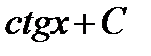 ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
24. Вычислить интеграл  :
:
А)  ; В)
; В)  ; С)
; С) 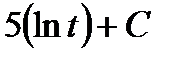 ; Д)
; Д) 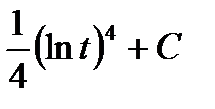 ; Е)
; Е) 
25. Вычислить интеграл  : А)
: А)  ; В)
; В)  ;
;
С)  ; Д)
; Д) 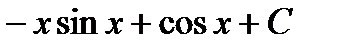 ; Е)
; Е) 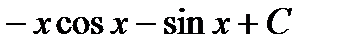
Дата добавления: 2015-08-26; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| IV. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ | | | Тюменская государственная медицинская академия |