СРСП №5 Кратные интегралы

Первые пять задач каждого варианта необходимо решить при следующих условиях: 1. Изменить порядок интегрирования в двойном интеграле. 2. Найти координаты центра тяжести однородной фигуры, ограниченной данными линиями. 3. Найти площадь части поверхности вырезаемой поверхностью . 4. Найти объем тела, ограниченного заданными поверхностями. 5. Найти массу тела плотности 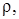ограниченного данными поверхностями.

Вариант № 1

1. .

2.

3. ,

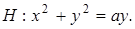
4.

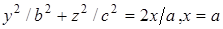
5.

6. Найти длину кардиоиды

7. Вычислить площадь части поверхности параболоида 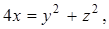ограниченной плоскостью

Вариант № 2

1.

2.

3.

4.

5.

6. Вычислить координаты центра тяжести однородной дуги астроиды расположенной в I квадранте.

7. Найти массу сферы если поверхностная плотность в каждой точке равна расстоянию от этой точки до оси .

Вариант № 3

1.

2.

3.

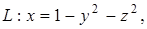
4.

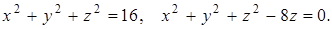
5.

6. Найти массу дуги окружности расположенной в I квадранте, если плотность распределения массы в каждой точке кривой равна квадрату ординаты.

7. Найти массу параболической оболочки , плотность которой в каждой точке равна ее аппликате.

Вариант № 4

1. .

2.

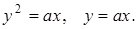
3. ,

4.

5.

6. Вычислить статический момент относительно плоскости одного витка винтовой линии

7. Найти площадь части поверхности сферы 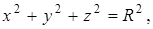расположенной внутри цилиндра

Вариант № 5

1.

2.

3.

4.

5.

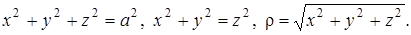
6. Вычислить момент инерции относительно точки дуги окружности

7. Найти площадь поверхности содержащейся между плоскостями

Вариант № 6

1. .

2.

3.

4.

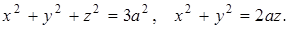
5. .

6. Вычислить статический момент относительно оси верхней половины эллипса если плотность распределения массы в точке равна ординате этой точки.

7. Найти массу поверхности сферы, если ее поверхностная плотность в каждой точке равна квадрату расстояния этой точки от вертикального диаметра.

Вариант № 7

1.

2.

3. ,

4.

5.

6. Вычислить массу отрезка , если и а плотность распределения массы в каждой точке равна

7. Найти статические моменты однородной треугольной пластинки относительно координатных плоскостей.

Вариант № 8

1.

2.

3. ,

4. содержащего точку

5.

6. Найти массу первого витка винтовой линии если плотность распределения массы в каждой точке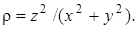

7. Найти момент инерции однородной треугольной пластинки относительно плоскости

Вариант № 9

1.

2.

3. ,

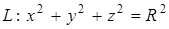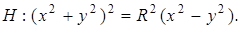
4.

5.

6. Найти массу одного витка однородной винтовой линии

7. Найти момент инерции однородной конической поверхности относительно плоскости .

Вариант № 10

1.

2.

3.

4.

5.

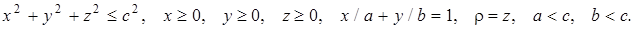
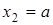6. Вычислить массу участка цепной линии между точками с абсциссами и , если плотность распределения массы в каждой точке обратно пропорциональна ординате точки, причем в точке плотность равна .

7. Вычислить момент инерции относительно оси однородной сферической оболочки плотность

Вариант № 11

1.

2.

3.

4.

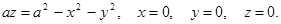
5.

6. Найти статический момент относительно оси дуги кривой

от до , если ее плотность

7. Найти массу полусферы если поверхностная плотность в каждой точке .

Вариант № 12

1.

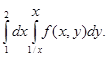
2.

3.

4.

5.

6. Вычислить момент инерции относительно начала координат четверти окружности, расположенной в первом квадранте, если плотность распределения массы

7. Найти площадь части поверхности сферы 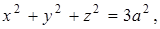заключенной внутри параболоида

Вариант № 13

1.

2.

3.

4.

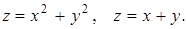
5.

6. Вычислить длину цепной линии между точками с абсциссами

7. Найти массу цилиндрической поверхности 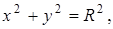заключенной между плоскостями если в каждой ее точке поверхностная плотность обратно пропорциональна квадрату расстояния ее до начала координат.

Вариант № 14

1.

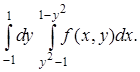
2.

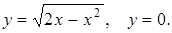
3.

4. содержащего точку

5.

6. Найти массу развертки окружности , если плотность распределения массы в точке равна расстоянию этой точки до начала координат.

7. Найти площадь части поверхности параболоида заключенного внутри цилиндра

Вариант № 15

1.

2.

3.

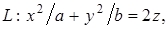
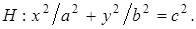
4.

5.

6. Найти массу кардиоиды , если плотность распределения массы в каждой точке равна ординате этой точки.

7. Найти площадь части поверхности ограниченную плоскостью

Дата добавления: 2015-08-27