Образец решения индивидуального задания. Задание 1. Составить формулу общего члена числового ряда:.

Задание 1. Составить формулу общего члена числового ряда: .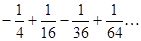

Решение. Во-первых, данный ряд является знакочередующимся, причём первый множитель является отрицательным. Поэтому формула общего члена ряда должна содержать множитель 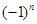. Во-вторых, все члены ряда представляют собой дроби со знаменателем, равным единице. В-третьих, знаменатели каждой дроби являются квадратами последовательных натуральных чётных чисел: 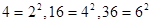и так далее. Таким образом, получим формулу: .

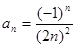Задание 2. Найти 8-й член числового ряда .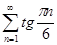

Решение. .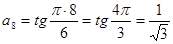

Задание 3. Найти частичную сумму 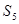числового ряда .

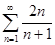Решение: .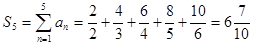

Задание 4. Исследовать на сходимость числовые ряды:

4.1. .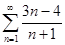

Решение. Проверим сначала для данного ряда выполнения необходимого условия сходимости: 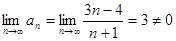. Предел общего члена ряда не равен нулю, следовательно, данный ряд является расходящимся.

4.2. .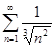

Решение. Данный ряд относится к типу обобщённых гармонических рядов 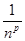, причём 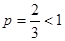, значит, ряд расходится.

4.3. .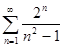

Решение. Используем признак Даламбера. Найдём 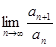. Здесь 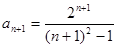. Получим: 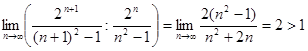. Согласно признаку Даламбера, данный ряд расходится.

4.4. .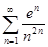

Решение. Применим радикальный признак Коши. Найдём 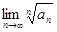. Получим: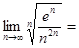

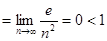. Согласно признаку Коши, данный ряд сходится.

4.5. .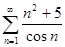

Решение. Проверим сначала для данного ряда выполнения необходимого условия сходимости: 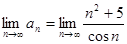. Числитель данной дроби стремится к бесконечности, а знаменатель – ограниченная величина, принимающая, в зависимости от 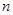значения различных знаков. Предел общего члена ряда, таким образом, не определён (и, естественно, не равен нулю), следовательно, данный ряд является расходящимся.

Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. .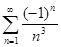

Решение. Запишем последовательность абсолютных величин членов данного ряда. Получим: 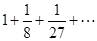. Члены ряда убывают по абсолютной величине. Теперь найдём предел общего члена ряда, составленного из абсолютных величин. Получим: 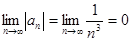- как предел обобщённого гармонического ряда при 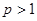. Таким образом, выполняются оба условия признака Лейбница, и данный ряд является сходящимся. Поскольку выше мы установили сходимость ряда, составленного из абсолютных величин, то данный ряд сходится абсолютно.

5.2. .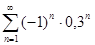

Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

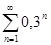. Он будет сходящимся, так как члены его составляют геометрическую прогрессию, знаменатель которой по модулю меньше единицы. Следовательно, данный ряд сходится, и сходится абсолютно.

Задание 6. Найти радиус, интервал и область сходимости ряда: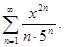

Решение. Запишем коэффициент данного ряда: 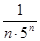. Найдём радиус сходимости данного ряда: 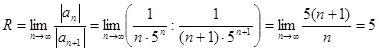. Интервал сходимости данного ряда будет 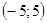. Проверим поведение ряда в конечных точках данного интервала.

Пусть 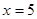. Получим ряд 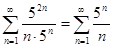. Проверим его сходимость по признаку Даламбера. 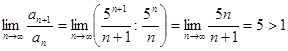. Ряд расходится, следовательно, точка 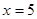не принадлежит области сходимости.

Пусть 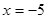. Получим ряд 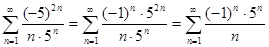. Получили знакочередующийся ряд, расходимость которого легко устанавливается с помощью признака Лейбница (не выполняется первое условие). То есть, точка 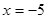также не входит в область сходимости. Итак, область сходимости данного ряда - .

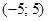Вариант № 1.

Задание 1. Составить формулу общего члена числового ряда: .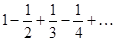

Задание 2. Найти 5-й член числового ряда .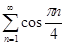

Задание 3. Найти частичную сумму 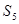числового ряда .

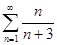Задание 4. Исследовать на сходимость числовые ряды:

4.1. 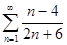. 4.2. 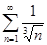. 4.3. 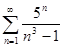. 4.4. 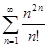. 4.5. .

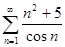Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 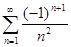. 5.2. .

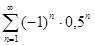Задание 6. Найти радиус, интервал и область сходимости ряда: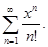

Вариант № 2.

Задание 1. Составить формулу общего члена числового ряда: .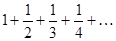

Задание 2. Найти 5-й член числового ряда .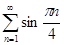

Задание 3. Найти частичную сумму 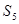числового ряда .

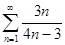Задание 4. Исследовать на сходимость числовые ряды:

4.1. 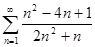. 4.2. 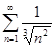. 4.3. 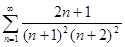. 4.4. 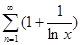. 4.5. .

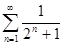Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 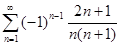. 5.2. .

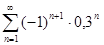Задание 6. Найти радиус, интервал и область сходимости ряда: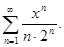

Вариант № 3.

Задание 1. Составить формулу общего члена числового ряда: .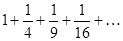

Задание 2. Найти 5-й член числового ряда .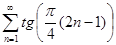

Задание 3. Найти частичную сумму 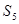числового ряда .

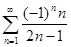Задание 4. Исследовать на сходимость числовые ряды:

4.1. 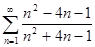. 4.2. 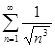. 4.3. 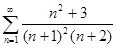. 4.4. 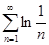. 4.5. .

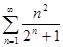Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 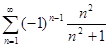. 5.2.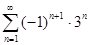

Задание 6. Найти радиус, интервал и область сходимости ряда: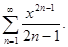

Вариант № 4.

Задание 1. Составить формулу общего члена числового ряда: .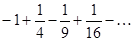

Задание 2. Найти 5-й член числового ряда .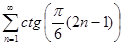

Задание 3. Найти частичную сумму 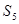числового ряда .

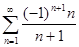Задание 4. Исследовать на сходимость числовые ряды:

4.1. 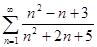. 4.2. 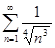. 4.3. 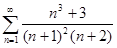. 4.4. 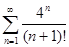. 4.5. .

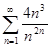Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 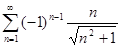. 5.2. .

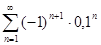Задание 6. Найти радиус, интервал и область сходимости ряда: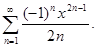

Вариант № 5.

Задание 1. Составить формулу общего члена числового ряда: .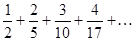

Задание 2. Найти 5-й член числового ряда .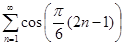

Задание 3. Найти частичную сумму 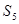числового ряда .

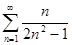Задание 4. Исследовать на сходимость числовые ряды:

4.1. 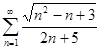. 4.2. 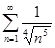. 4.3. 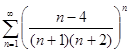. 4.4. 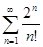. 4.5. .

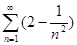Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 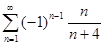. 5.2. .

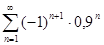Задание 6. Найти радиус, интервал и область сходимости ряда: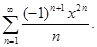

Вариант № 6.

Задание 1. Составить формулу общего члена числового ряда: .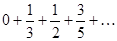

Задание 2. Найти 5-й член числового ряда .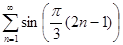

Задание 3. Найти частичную сумму 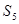числового ряда .

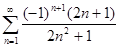Задание 4. Исследовать на сходимость числовые ряды:

4.1. 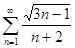. 4.2. 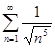. 4.3. 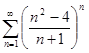. 4.4. 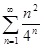. 4.5. .

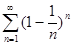Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 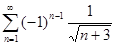. 5.2. .

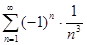Задание 6. Найти радиус, интервал и область сходимости ряда: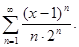

Вариант № 7.

Задание 1. Составить формулу общего члена числового ряда: .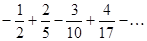

Задание 2. Найти 5-й член числового ряда .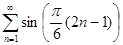

Задание 3. Найти частичную сумму 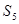числового ряда .

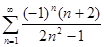Задание 4. Исследовать на сходимость числовые ряды:

4.1. 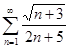. 4.2. 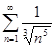. 4.3. 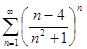. 4.4. 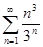. 4.5. .

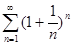Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 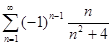. 5.2. .

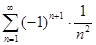Задание 6. Найти радиус, интервал и область сходимости ряда: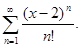

Вариант № 8.

Задание 1. Составить формулу общего члена числового ряда: .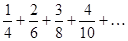

Задание 2. Найти 5-й член числового ряда .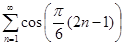

Задание 3. Найти частичную сумму 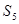числового ряда .

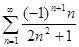Задание 4. Исследовать на сходимость числовые ряды:

4.1. 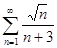. 4.2. 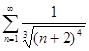. 4.3. 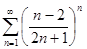. 4.4. 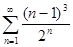. 4.5. .

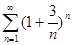Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 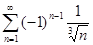. 5.2. .

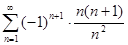Задание 6. Найти радиус, интервал и область сходимости ряда: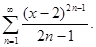

Вариант № 9.

Задание 1. Составить формулу общего члена числового ряда: .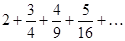

Задание 2. Найти 5-й член числового ряда .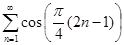

Задание 3. Найти частичную сумму 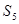числового ряда .

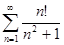Задание 4. Исследовать на сходимость числовые ряды:

4.1. 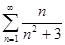. 4.2. 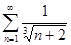. 4.3. 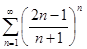. 4.4. 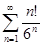. 4.5. .

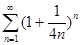Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 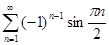. 5.2. .

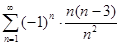Задание 6. Найти радиус, интервал и область сходимости ряда: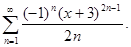

Вариант № 10.

Задание 1. Составить формулу общего члена числового ряда: .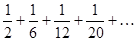

Задание 2. Найти 5-й член числового ряда .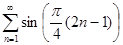

Задание 3. Найти частичную сумму 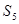числового ряда .

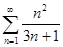Задание 4. Исследовать на сходимость числовые ряды:

4.1. 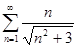. 4.2. 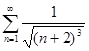. 4.3. 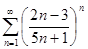. 4.4. 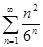. 4.5. .

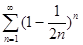Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 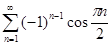. 5.2. .

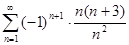Задание 6. Найти радиус, интервал и область сходимости ряда: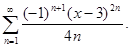

Вариант № 11.

Задание 1. Составить формулу общего члена числового ряда: .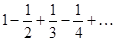

Задание 2. Найти 5-й член числового ряда .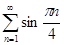

Задание 3. Найти частичную сумму 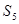числового ряда .

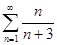Задание 4. Исследовать на сходимость числовые ряды:

4.1. 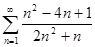. 4.2. 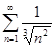. 4.3. 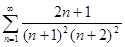. 4.4. 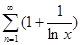. 4.5. .

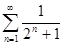Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 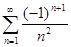. 5.2.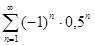

Задание 6. Найти радиус, интервал и область сходимости ряда: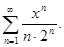

Вариант № 12.

Задание 1. Составить формулу общего члена числового ряда: .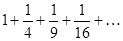

Задание 2. Найти 5-й член числового ряда .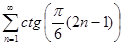

Задание 3. Найти частичную сумму 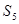числового ряда .

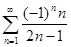Задание 4. Исследовать на сходимость числовые ряды:

4.1. 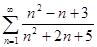. 4.2. 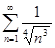. 4.3. 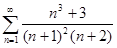. 4.4. 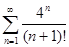. 4.5. .

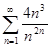Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 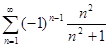. 5.2. .

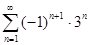Задание 6. Найти радиус, интервал и область сходимости ряда: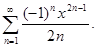

Вариант № 13.

Задание 1. Составить формулу общего члена числового ряда: .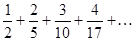

Задание 2. Найти 5-й член числового ряда .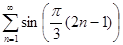

Задание 3. Найти частичную сумму 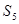числового ряда .

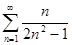Задание 4. Исследовать на сходимость числовые ряды:

4.1. 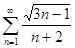. 4.2. 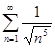. 4.3. 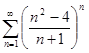. 4.4. 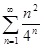. 4.5. .

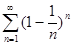Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 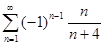. 5.2. .

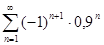Задание 6. Найти радиус, интервал и область сходимости ряда: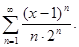

Вариант № 14.

Задание 1. Составить формулу общего члена числового ряда: .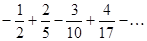

Задание 2. Найти 5-й член числового ряда .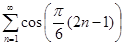

Задание 3. Найти частичную сумму 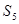числового ряда .

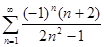Задание 4. Исследовать на сходимость числовые ряды:

4.1. 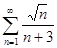. 4.2. 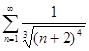. 4.3. 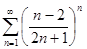. 4.4. 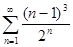. 4.5. .

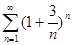Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 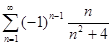. 5.2. .

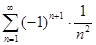Задание 6. Найти радиус, интервал и область сходимости ряда: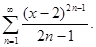

Вариант № 15.

Задание 1. Составить формулу общего члена числового ряда: .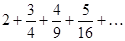

Задание 2. Найти 5-й член числового ряда .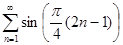

Задание 3. Найти частичную сумму 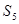числового ряда .

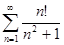Задание 4. Исследовать на сходимость числовые ряды:

4.1. 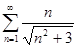. 4.2. 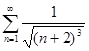. 4.3. 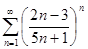. 4.4. 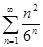. 4.5. .

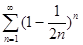Задание 5. Исследовать на сходимость знакопеременные ряды:

5.1. 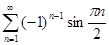. 5.2. .

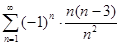Задание 6. Найти радиус, интервал и область сходимости ряда: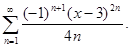

Дата добавления: 2015-08-27