СРСП №1 Дифференциальное исчисление функций одной переменной

ОБРАЗЕЦ РЕШЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Решение:

Воспользуемся формулой: . Для данной функции получим: .

Ответ: .

Задание 2. Найти производные функций:

2.1.

Решение:

.

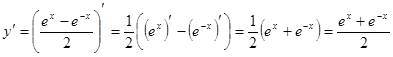. 2.2. .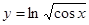

Решение:

Используем правило дифференцирования сложной функции: .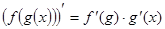

.

Заметим, что этот результат можно было получить, представив функцию в виде .

2.3. .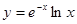

Решение:

Воспользуемся правилом дифференцирования произведения двух функций: 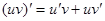. Получим .

2.4. .

Решение:

Снова используем формулу производной сложной функции: 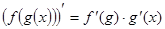. Получим: .

Задание 3. Продифференцировать неявно заданную функцию .

Решение:

Продифференцируем обе части данного уравнения по переменной , учитывая при этом, что является функцией аргумента . Получим:

. Из полученного равенства выразим производной : , откуда .

Задание 4. Продифференцировать функцию, заданную параметрически:

Решение:

Используем правило дифференцирования функции, заданной параметрически: . Получим: .

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .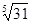

Решение:

Используем приближённое равенство: , верное при малых значениях . Откуда: .

Преобразуем сначала исходное выражение: . Положим , , . Производная равна: , . Окончательно имеем: .

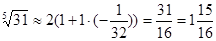Задание 6. Найти вторую производную функции .

Решение:

Сначала находим первую производную: .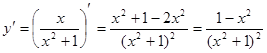

Вычисляем вторую производную:

.

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Решение:

Запишем уравнение касательной: . В нашем случае , . Подставляем в уравнение: , откуда - уравнение касательной.

Запишем уравнение нормали: . Подставив в это уравнение числовые данные: , откуда - уравнение нормали.

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Решение:

Запишем общую формулу логарифмической производной: 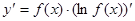. В нашем случае: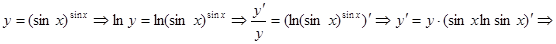

Задание 9. Исследовать функцию и построить ее график:

Решение.

Функция определена и непрерывна в интервале (0;+¥). В граничной точке 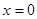области определения функция имеет бесконечный разрыв, так как .

Так как в точке 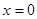функция имеет бесконечный разрыв, то прямая 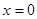является вертикальной асимптотой. Найдем уравнение наклонной асимптоты (если она существует).

;

.

(При нахождении пределов воспользовались правилом Лопиталя).

Итак, и уравнение асимптоты . Таким образом, график имеет в качестве асимптот оси координат.

Найдем производную функции и критические точки:

. Стационарная критическая точка: . Исследуем знак производной на интервалах(0;е) и (е;¥).

Составим таблицу:

Экстремум функции: .

Найдем вторую производную и значения х, при которых график может иметь точку перегиба:

, при .

Определим знак второй производной в интервалах и

+

-

:

Составим таблицу:

y(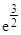)=3/()» 0,33

График пересекает ось абсцисс в точке (1;0). Точек пересечения с осью ординат нет. Строим эскиз графика функции:

	е

	е

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Решение:

Найдём область определения функции: . Далее, продифференцируем функцию: . Найдём критические точки: . Одна из них, , принадлежит рассматриваемому промежутку. Определим значение функции в границах отрезка и в этой точке:

. Таким образом, .

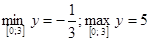Вариант № 1.

Задание 1. Вычислить приращение функции 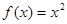в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. 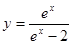. 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию .

Задание 4. Продифференцировать функцию, заданную параметрически:

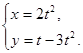
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .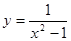

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .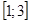

Вариант № 2.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. 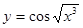. 2.3. 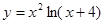. 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

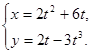
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции 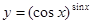с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции 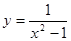на отрезке .

Вариант № 3.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

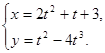
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .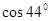

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции 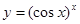с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 4.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

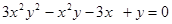Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .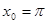

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 5.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .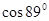

Задание 6. Найти вторую производную функции .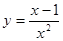

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .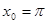

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 6.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

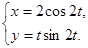
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 7.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. 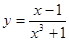. 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

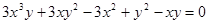Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .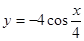

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 8.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. 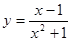. 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

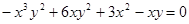Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции 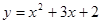в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 9.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .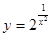

Задание 3. Продифференцировать неявно заданную функцию:

.

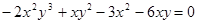Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции 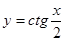на отрезке .

Вариант № 10.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции 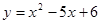в точке .

Задание 8. Найти производную функции 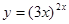с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .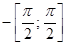

Вариант № 11.

Задание 1. Вычислить приращение функции 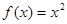в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. 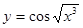. 2.3. 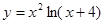. 2.4. .

Задание 3. Продифференцировать неявно заданную функцию .

Задание 4. Продифференцировать функцию, заданную параметрически:

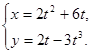
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции 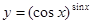с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции 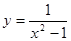на отрезке .

Вариант № 12.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .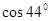

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 13.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

Задание 4. Продифференцировать функцию, заданную параметрически:

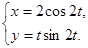
Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .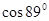

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .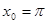

Задание 8. Найти производную функции с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 14.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. 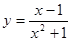. 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

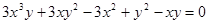Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции с помощью логарифмического дифференцирования

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .

Вариант № 15.

Задание 1. Вычислить приращение функции в точке , соответствующее приращению аргумента .

Задание 2. Найти производные функций:

2.1. . 2.2. . 2.3. . 2.4. .

Задание 3. Продифференцировать неявно заданную функцию:

.

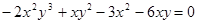Задание 4. Продифференцировать функцию, заданную параметрически:

Задание 5. Вычислить с помощью дифференциала приближённое значение выражения .

Задание 6. Найти вторую производную функции .

Задание 7. Составить уравнения касательной и нормали к графику функции в точке .

Задание 8. Найти производную функции 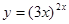с помощью логарифмического дифференцирования.

Задание 9. Исследовать функцию и построить схематически её график.

Задание 10. Найти наибольшее и наименьшее значение функции на отрезке .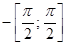

Дата добавления: 2015-08-27