Анализ алгоритмов затраты по объему памяти и времени, стандартные классы сложности

Традиционно в программировании понятие сложности алгоритма связано с использованием ресурсов компьютера: насколько много процессорного времени требует программа для своего выполнения, насколько много при этом расходуется память машины? Учет памяти обычно ведется по объему данных и не принимается во внимание память, расходуемая для записи команд программы. Время рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для машин с разной тактовой частотой и с незначительными вариациями в архитектуре.

Такой подход сложился исторически и ориентируется, прежде всего, на научные и инженерные приложения теории алгоритмов: объемы данных значительно превышают размеры самой программы, а программа может выполняться несколько часов. Если не считать офисных и бухгалтерских применений вычислительных машин, то производительность и объем памяти компьютера никогда не казались программистам чрезмерными и постоянной задачей является сделать программу работающей хотя бы немного быстрее и попытаться заставить ее работать в стесненных условиях ограниченного поля памяти.

Если в научных и инженерных приложениях большое время вычислений доставляет лишь неудобство пользователям, то в ряде других областей ресурсы настолько критичны, что может возникнуть проблема целесообразности всего проекта из-за неэффективной работы программы. К таким областям относятся системы реального времени (real-time systems), которые управляют процессами в реальном мире или обрабатывают информацию, служащую для принятия оперативных решений. Примерами систем реального времени являются бортовые компьютерные системы космических кораблей, самолетов, других транспортных средств; компьютерные системы, управляющие непрерывным химическим производством, ядерными реакторами; системы противовоздушной обороны, управления огнем и др.

Существует ряд важных практических причин, побуждающих нас заниматься анализом алгоритмов. Одной из них является потребность получения оценок или границ для объема памяти и времени работы, необходимых алгоритму для успешной обработки входных данных. Следует избегать разработки программы, которая за отведенное студенту машинное время не успеет обработать входные данные достаточно большого размера (например, следует признать неудовлетворительной программу обработки графов, если из-за нехватки времени она не дает ответа для графа, состоящего из десяти вершин). Лучше заранее (еще при разработке алгоритма) с помощью карандаша и бумаги оценить объем памяти и время, необходимые разрабатываемому алгоритму, а затем улучшать его (или разработать новый, более эффективный). Хороший анализ может выявить узкие места в ваших программах (например, те части программы, на выполнение которых расходуется большая часть времени), а также выбрать более подходящий алгоритм из широкого класса алгоритмов, решающих одно и то же задание.

Одну и ту же задачу могут решать много алгоритмов. Эффективность работы каждого из них описывается разнообразными характеристиками. Прежде чем анализировать эффективность алгоритма, нужно доказать, что данный алгоритм правильно решает задачу, а потом решать, насколько это решение эффективно.

При анализе алгоритма определяется количество «времени», необходимое для его выполнения. Это не реальное число секунд или других промежутков времени, а приблизительное число операций, выполняемых алгоритмом. Число операций и измеряет относительное время выполнения алгоритма. Таким образом, иногда «временем» называют вычислительную сложность алгоритма. Фактическое количество секунд, требуемое для выполнения алгоритма на компьютере, непригодно для анализа, т.к. обычно интересует только относительная эффективность алгоритма, решающего конкретную задачу. Действительно, время, требуемое на решение задачи,- не очень хороший способ измерять эффективность алгоритма, потому что алгоритм не становится лучше, если его исполнять на более медленном.

На самом деле фактическое количество операций алгоритма на тех или иных входных данных не представляет большого интереса и не очень много сообщает об алгоритме. Реально определяется зависимость числа операций конкретного алгоритма на тех или иных входных данных. Можно сравнить два алгоритма по скорости роста числа операций. Именно скорость роста играет ключевую роль, поскольку при небольшом размере входных данных алгоритм А может требовать меньшего количества операций, чем алгоритм В, но при росте объема входных данных ситуация может поменяться на противоположную.

Для алгоритма A мы определили функцию временной сложности ВРЕМЯ А(n), дающую верхнюю границу для максимального времени его работы. Эта функция зависит от максимального числа основных операций (сложения, сравнения и т.д.), которые должен выполнить алгоритм при решении задачи на входных данных размером n. Аналогично можно определить функцию емкостной сложности ПАМЯТЬ А (n), дающую границу для максимального числа одновременно существующих скалярных значений при выполнении А на входных данных размером n.

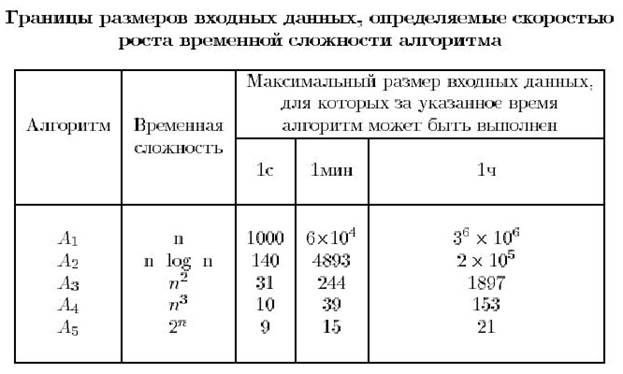
Хорошим критерием качества алгоритма является скорость роста его сложности в зависимости от увеличения размера входа. В таблицах 1 и 2 показано влияние порядка роста сложности алгоритма на увеличение максимально допустимого размера входных данных, которого можно достичь увеличением скорости ЭВМ, а также эффект применения более эффективного. В общем случае следует иметь в виду, что повышение скорости работы алгоритма может потребовать увеличения необходимой ему памяти. Например, рекурсивный алгоритм порождения перестановок в порядке минимального изменения совсем не производит сравнений, но имеет емкостную сложность, в то время как емкостная сложность нерекурсивного алгоритма равна. Этот же пример показывает справедливость обратного утверждения: за счет увеличения временной сложности алгоритма можно понизить его емкостную сложность.

Как правило, более эффективный алгоритм приводит к программе большего размера и требует больших усилий, как на его разработку, так и на его обоснование.

Дата добавления: 2015-08-27