Решение. 1.Модель представляет собой систему взаимосвязанных (одновременных) уравнений

1. Модель представляет собой систему взаимосвязанных (одновременных) уравнений. Проверим каждое ее уравнение на идентификацию.

Необходимое условие идентификации – выполнение счетного правила:

D +1 = H – уравнение идентифицируемо;

D +1 < H – уравнение неидентифицируемо;

D +1 > H – уравнение сверхидентифицируемо,

где H – число эндогенных переменных в уравнении;
D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.

Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели (системы) у.

Экзогенные переменные – независимые переменные, которые определяются вне системы х.

Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.

Коэффициенты a и b при переменных – структурные коэффициенты модели.

Данная модель включает четыре эндогенные переменные () и пять преопределенных переменных (две экзогенные переменные – P_t и R_t и три лаговые эндогенные переменные – Y_t-1, C_t-1 и Q_t-1).

Проверим необходимое условие идентификации для уравнений модели.

I-е уравнение.
Это уравнение включает две эндогенные переменные (Y_t и I_t) и одну преопределенную переменную (Y_t-1). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 4+1 > 2. Уравнение сверхидентифицировано.

II-е уравнение.
Это уравнение включает три эндогенные переменные (Q_t, Y_t и I_t) и ноль преопределенных переменных. Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 5+1 > 3. Уравнение сверхидентифицировано.

III-е уравнение.
Это уравнение включает одну эндогенную переменную (C_t) и две преопределенные переменные (P_t и C_t-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1 > 1. Уравнение сверхидентифицировано.

IV-е уравнение.
Это уравнение включает одну эндогенную переменную (Q_t) и две преопределенных переменных (R_t и Q_t-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1 > 1. Уравнение сверхидентифицировано.

Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12
II уравнение	b21		-1	b22
III уравнение					-1	b31	b33
IV уравнение				-1				b41	b42

В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т.е. 4-1=3.

I-е уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

.

Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:

Достаточное условие идентификации для первого уравнения выполняется.

II-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12
II уравнение	b21		-1	b22
III уравнение					-1	b31	b33
IV уравнение				-1				b41	b42

.

Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:

Достаточное условие идентификации для второго уравнения выполняется.

III-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12
II уравнение	b21		-1	b22
III уравнение					-1	b31	b33
IV уравнение				-1				b41	b42

.

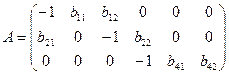Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:

Достаточное условие идентификации для третьего уравнения выполняется.

IV-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12
II уравнение	b21		-1	b22
III уравнение					-1	b31	b33
IV уравнение				-1				b41	b42

.

Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:

Достаточное условие идентификации для четвертого уравнения выполняется.

Таким образом, все уравнения модели сверхидентифицированы.

2.

Приведенная форма модели – это система линейных функций эндогенных переменных от всех предопределенных переменных системы:

Запишем приведенную форму заданной модели в общем виде:

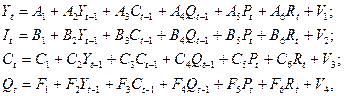
где V₁, V₂, V₃ и V₄ – случайные ошибки.

21. Макроэкономическая модель кейнса

Кейнсианские модели роста используют в основном тот же логический подход, но теперь анализ со стороны спроса соединен с факторами, определяющими динамику предложения, и выясняются условия динамического равновесия спроса и предложения в экономике. Стратегической переменной, с помощью которой можно управлять экономическим ростом являются инвестиции.

Кейнс подверг критике ряд постулатов классической теории. В первую очередь это относится к вопросу об уровне занятости и факторах безработицы. Считалось, что спрос и предложение на рынке труда регулируются ставкой заработной платы, что безработица существует только в двух типах: фрикционная, причина которой – плохая информированность трудящихся о предложении рабочих мест, и добровольная, возникающая, когда рабочие не хотят трудиться за предлагаемую зарплату

Кейнс пришел к заключению, что денежная заработная плата не участвует в регулировании рынка труда. Под влиянием профсоюзов и других социальных факторов зарплата вообще может не снижаться. Это значит, что если предложение труда опережает спрос на него, возникает безработица, причем вынужденная.

Далее Кейнс выступил с критикой закона рынков Сэя, который утверждал, что производство само формирует доходы, обеспечивая соответствующий спрос на товары, и исключает общее перепроизводство товаров и услуг. Кейнс указал, что подобная позиция правомерна лишь для бартерного обмена. В денежной экономике цены не успевают выравнивать спрос и предложение в силу действия «эффекта храповика». Может возникнуть и реально возникает общее перепроизводство. Именно за счет увеличения безработных в системе восстанавливается равновесие. В теории Кейнса оказывается возможным общее равновесие при неполной занятости.

Кейнс приходит к выводу о том, что размеры общественного производства и занятости, их динамика определяются не факторами предложения, а факторами платежеспособного спроса. Кейнс вводит понятия функций совокупного спроса и совокупного предложения. Первая функция определяется соотношением между ожидаемыми доходами предпринимателей и объемом занятости, вторая – между совокупными издержками и совокупной занятостью. Точка пересечения функций как раз и определяет объем занятости в масштабах всего общества («точка эффективного спроса»). Эффективный спрос – это, по Кейнсу, совокупный платежеспособный спрос, определяющий объем занятости. Главными компонентами эффективного спроса выступают потребление и инвестиции.

Анализ эффективного спроса основывается на понятиях «склонность к потреблению» и «склонность к сбережению». По Кейнсу, доход является основным фактором, определяющим потребление и сбережения. С ростом доходов растет и спрос, увеличиваются расходы на потребление, но не в той пропорции, в которой увеличивается доход. В качестве причины выступает «основной психологический закон», смысл которого состоит в том, что по мере роста дохода, увеличения богатства склонность к потреблению снижается. Это связано с ростом расходов на покупку дорогостоящих предметов длительного пользования, что требует сбережения, накопления части дохода.

Кейнс создает простую макроэкономическую модель рынка:

Y = C + S,

где Y – доход; С – потребление; S – сбережение.

Он применяет следующие формулы:

доход = ценности продукции = потреблению + инвестиции
(Y = C + I);

сбережение = доходу – потребление (S = Y – C);

сбережения = инвестициям (S = I).

Неравенство этих величин рассматривается как признак нарушения экономического равновесия.

Размеры сбережений, считает Кейнс, регулирует не процентная ставка, как думали классики, а различные мотивы и соображения людей: чтоб делать крупные покупки, иметь запас наличных денег для непредвиденных покупок («предпочтение ликвидности»), для будущего потребления, непредвиденных случаев и т.д.

Из основного психологического закона Кейнса следует, что при росте дохода доля эффективного спроса, обеспечиваемая личным потреблением, все время падает и поэтому расширяющийся объем сбережений должен постоянно поглощаться растущим спросом на инвестиции. Размер инвестиций Кейнс считал главным фактором эффективного спроса, а через его посредство – главным фактором занятости и национального дохода. Важно, чтобы перевести все сбережения в инвестиции. Классики не видели здесь особой проблемы. Кейнс, напротив, полагал, что создание объема инвестиций, необходимого для полной занятости, составляет сложную проблему, важнейшую задачу экономической политики государства.

Оказалось, что при росте дохода потребление сокращается, сбережения растут, а инвестиции могут и не увеличиваться. Росту инвестиций препятствует снижение нормы ожидаемой прибыли, которое зависит от действия закона убывающей производительности капитала. Уровень инвестиций зависит от нормы прибыльности и процентной ставки. Ожидаемая предпринимателями прибыль будет наибольшей в точке эффективного спроса.

Объем инвестиций зависит, по Кейнсу, от побуждения к инвестированию. Предприниматель расширяет свои инвестиции, пока предельная эффективность капитала (норма прибыли) падает до уровня процента. Источник экономических трудностей в том, что рентабельность капитала снижается сильно, тогда как норма процента сохраняет устойчивость. Это создает узкие границы для новых инвестиций и тем самым для роста занятости.

Снижение предельной эффективности капитала Кейнс объясняет прежде всего значительной аккумуляцией капиталов. Огромное значение он придает психологическому фактору – видам предпринимателей на будущие доходы («перспективная выгода»). Наступление экономических кризисов Кейнс выводит из «кризиса доверия», из потери капиталистами веры в будущие доходы.

В теории Кейнса намечена количественная связь между инвестициями и национальным доходом. Она представляется так называемым мультипликационным эффектом, который под влиянием приращения инвестиций в одной из отраслей вызывает приращение потребления и дохода не только в данной отрасли, но и в сопряженных отраслях. Итоговое приращение национального дохода оказывается больше первоначальной суммы инвестиций. Это выражается формулами:

где ∆Y – прирост дохода;

∆I – прирост инвестиций;

К – мультипликатор.

Мультипликатор оказывается функцией предельной склонности к сбережению. Следовательно, теория мультипликатора базируется на предельных величинах. Это существенная методологическая особенность всей концепции макроэкономической динамики.

Теория процента с другой стороны объясняет проблему инвестирования и занятости. В основе процента лежит, по Кейнсу, особый психологический мотив, обозначаемый как «предпочтение ликвидности». Суть мотива – в стремлении удержать богатство в наиболее ликвидной, т.е. денежной форме. Процент – компенсация за отказ от этой наиболее ликвидной формы богатства.

22-24Модель Домара, Харрада, харрада-Домара

ля того чтобы выяснить роль увеличения производственных мощностей, связанного с осуществлением чистых инвестиций, в модели Домара предполагается, что кейнсианское условие краткосрочного равновесия - равенство намечаемых сбережений планируемым инвестициям - уже соблюдено (S=I). ¹ Кроме того, предполагается, что сбережения и инвестиции составляют s, постоянную долю национального продукта:

S = I = sY, 0 < s < l, (1)

где

s ≡ S/Y ≡ ΔS/ΔY, где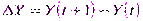

Таким образом, s характеризует угол наклона функции и долгосрочных сбережений, которая проходит через начало координат. Поскольку угол наклона такой линии совпадает с отношением координат соответствующей точки, величина предельной склонности к сбережению, ΔS/ΔY, совпадает со значением средней склонности к сбережению S/Y.

Y обозначает физический объем годового национального дохода (все потоки здесь и далее определены в годовом исчислении). Предполагается, что размеры национального продукта достаточны для того, чтобы полностью привести в действие наличный запас капитальных благ (с должной поправкой на резервные мощности). Таким образом, мы можем считать Y национальным продуктом при условии полного использования производственных мощностей.

Итак, инвестиции текущего года, фигурирующие в уравнении (1), вызовут расширение производственных мощностей; масштабы такого расширения могут быть описаны следующим образом: σ I = σ sY. Коэффициент σ - показатель капиталоотдачи, величина, обратная определяемому технологическими условиями предельному отношению капитал-продукт ΔK/ΔY ≡ I/ΔY. Другими словами,

σ ≡ ΔY/ΔK ≡ ΔY/I,

где К - капитальный запас, а ΔK, следовательно, равно величине чистых инвестиций. Другими словами, коэффициент σ представляет собой среднее потенциальное годовое увеличение национального продукта, ставшее возможным благодаря инвестированию одного доллара или соответствующему росту капитального запаса, сочетающемуся с другими наличными ресурсами, главным образом с трудом. Отсюда σ I - потенциальное увеличение годового национального продукта (т. е. увеличение производственной мощности), вызванное инвестициями данного года, I. Чтобы это увеличение производственного потенциала не повлекло за собой простого наращивания избыточных мощностей и тем самым не стало бы сдерживать будущие инвестиции и рост национального продукта, необходимо удовлетворить следующее условие:

ΔY = σ I. (2)

Национальный доход (совокупные расходы) будущего года должен вырасти по сравнению с уровнем данного года на величину, равную добавочной производственной мощности, обеспечиваемой I.

Из кейнсианской теории мультипликатора следует, что увеличение инвестиций вызывает рост национального дохода(Y=S+I). В самом деле, при данной склонности к сбережению s, увеличение годового дохода ΔY, сопряженное с ростом годовых инвестиций на ΔI, может быть выражено в таком виде:

ΔY = ΔI·1/s, (3)

где l/s представляет собой мультипликатор. Тогда, подставляя уравнение (3) в уравнение (2), получим:

ΔI·1/s = σ I. (4)

Разделив обе части выражения (4) на I и умножив их на s, получаем

ΔI/I = σ s. (5)

При фиксированной величине капиталоотдачи и данной склонности к сбережению полное использование ежегодного прироста производственных мощностей в рамках всей экономики достигается при росте инвестиций (по принципу сложных процентов) ежегодным темпом, равным σ s. Темп роста, равный σ s,- это темп равновесного экономического роста, или темп хозяйственного роста при полной загрузке производственных мощностей.

Поскольку предполагалось, что инвестиции (и сбережения) составляют постоянную долю национального продукта, из этого необходимо следует, что последний тоже должен расти темпом, равным σ s (процентов). Если это сразу не кажется очевидным, читатель может подставить σ sY вместо σ Y в выражение (2), тогда, разделив обе части выражения на Y, нетрудно убедиться в том, что действительно

ΔY/Y = σ s или .

Преобразуя, мы получаем окончательное уравнение динамики национального дохода:

Y (t + 1) = (1 + σs) Y(t).

Эта модель представляет собой конечно-разностное уравнение первого порядка. Если предположить Y(0)=Y₀, то тогда Y(1)=(1+σs)Y₀

Y(2)=(1+σs)Y1=(1+ σs)²Y₀

и т.д.

Таким образом, общее решение имеет вид

Y(t)= (1+σs)^tY₀

Принимая s равным, например, 0,12 и σ = 1/з (что соответствует значению коэффициента капитал - продукт, равному 3), получим, что при полной загрузке производственных мощностей темп роста экономики равен 4% в год.

Ясно, что темп роста экономики при полной загрузке производственных мощностей изменяется прямо пропорционально s и σ. Это вполне естественно, поскольку, чем большая доля s национального продукта сберегается и инвестируется (при данном коэффициенте капиталоотдачи), тем больше увеличиваются производственные мощности, создаваемые благодаря этим инвестициям, и, следовательно, тем выше должны быть темпы роста национального продукта, препятствующие недоиспользованию производственных мощностей. Аналогичным образом: чем больше σ, тем больше при любом заданном размере инвестиций увеличение производственных мощностей и, следовательно, тем значительней должен быть рост национального продукта, который предотвращает образование избыточных мощностей.

Более тщательный разбор описываемой модели показывает, что условия равновесного роста экономики (или роста в условиях полной загрузки мощностей) в неявном виде заключают в себе уже знакомое нам кейнсианское условие равенства намечаемых сбережений планируемым инвестициям, но только здесь это условие перенесено с краткосрочного периода (когда размеры капитального запаса фиксированы) на долгосрочный (когда такой запас оказывается переменной величиной). Итак, отправной точкой анализа в рамках такой модели роста служит кейнсианское условие краткосрочного равновесия сбережений и инвестиций (S=I). Кроме того, эта модель содержит следующее требование: для реализации приращения продукта, вызванного данными инвестициями, на ту же величину должен вырасти и национальный доход. Но анализ мультипликационного механизма показывает, что этот результат может быть достигнут только с помощью дополнительных инвестиций. Размеры такого увеличения зависят от предельной склонности к сбережению, и, таким образом, мы снова приходим к соотношению (4).

Перепишем это уравнение в следующем виде:

ΔI = σ sI.

Поскольку увеличение потенциального продукта, которому должно соответствовать увеличение дохода или спроса, можно описать как σ I = ΔY, то равенство ΔI = σ sI превращается в

ΔI = sΔY = ΔS.

Иначе говоря, условием равновесного роста экономики при расширяющемся капитальном запасе является сохранение первоначального равенства сбережений и инвестиций при совпадении между собой всех дальнейших приростов сбережений и инвестиций.

Обратим внимание еще на один аспект формулировки условий устойчивого, равновесного роста в модели Домара. Согласно ей, рост инвестиций (и дохода) задается создающим производственные мощности и мультипликативным (доходообразующим) эффектами инвестиций; при этом ничего не говорится о факторах, определяющих инвестиции, другими словами, отсутствует уравнение спроса на инвестиции - уравнение, которое могло бы дать нам какое-нибудь представление об их фактическом поведении.

---

Дата добавления: 2015-08-17