Изучение сезонных колебаний

При анализе данных многих социально-экономических явлений за определенный интервал времени обнаруживаются определенные повторяющиеся колебания, которые не изменяются длительный период времени. Они являются результатом действия природно-климатических условий, общих экономических факторов и других экономических факторов, частично регулируемых. В статистике такие колебания называются сезонными. Это особый тип динамики. Сезонность можно понимать как внутригодовую динамику вообще. Сезонность может возникать в отраслях, связанных с переработкой сельхозсырья, в торговле из-за сезонного характера спроса на товары и т.д. Таким образом, периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название " сезонные колебания " или " сезонные волны ", а динамический ряд в этом случае называют сезонным рядом динамики.

При статистическом изучении в рядах внутригодовой динамики сезонных колебаний, решаются следующие две взаимосвязанные задачи:

1. выявление специфики развития изучаемого явления во внутригодовой динамике;

2. измерение сезонных колебаний изучаемого явления с построением модели сезонной волны.

На специфику изменения уровней рядов внутригодовой динамики могут оказывать влияние как факторы, образующие их составные компоненты (тренд, периодические колебания, случайные отклонения), так и внешние причины, обусловленные характером сбора и обработки исходной информации.

Статистические ряды внутригодовой динамики обычно составляются по материалам текущей отчетности. Одним из непременных условий статистического изучения сезонных колебаний является то, что ряды динамики должны быть приведены к сопоставимому виду. При этом надо иметь в виду, что разновеликие по продолжительности месяцы и кварталы годовых периодов являются одной из причин, влияющих на изменения уровней рядов внутригодовой динамики. Для устранения этой причины объемные величины пересчитываются в средние величины, характеризующие интенсивность развития изучаемого явления в единицу времени. Это имеет важное значение для повышения точности показателей сезонных колебаний.

В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности i _S. Совокупность этих показателей отражает сезонную волну. В общем виде они определяются отношением исходных (эмпирических) уровней ряда динамики (у_i) к теоретическим (расчетным) уровням (у_t), выступающим в качестве базы сравнения:

Именно в результате того, что в этой формуле измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда (у_t), в исчисляемых при этом индивидуальных индексах сезонности, влияние основной тенденции развития элиминируется (устраняется).

Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.

Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности:

Вычисленные на основе этой формулы средние индексы сезонности (с применением, в качестве базы сравнения, соответствующих уровней тренда) свободны от влияния основной тенденции развития и случайных отклонений. (см. Сезонная корректировка временного ряда)

В зависимости от характера тренда, формула принимает следующие формы:

1) Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития (т.н. нестационарные ряды динамики). Выступающие при этом, в качестве переменной базы сравнения, теоретические уровни (у_t) представляют, своего рода, "среднюю ось кривой", так как их расчет основан на положениях метода наименьших квадратов. Поэтому измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней.

2) Для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен (т. н. стационарные ряды динамики). В данной формуле базой сравнения является общий для анализируемого ряда динамики средний уровень. Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы называется способом постоянной средней. К оэффициент сезонности или индекс сезонности, в данном случае представляет собой отношение средней из фактических уровней одноименных месяцев к средней из выровненных (теоретических, расчетных) данных по тем же месяцам, выступающим в качестве базы сравнения: (см. Анализ сезонных колебаний. Индекс сезонности. Метод абсолютных и относительных разностей).

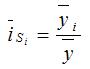Для определения теоретических уровней тренда важно правильно подобрать математическую функцию, по которой будет производиться аналитическое выравнивание в анализируемом ряду динамики. Это наиболее сложный и ответственный этап изучения сезонных колебаний. От обоснованности подбора той или иной математической функции, во многом зависит практическая значимость получаемых в анализе индексов сезонности.

При использовании способа аналитического выравнивания ход вычислений индексов сезонности следующий:

1. - по соответствующему полиному вычисляются для каждого месяца (квартала) выравненные уровни на момент времени t;

2. - определяются отношения фактических месячных (квартальных) данных к соответствующим выравненным данным (в процентах, долях);

3. - находятся средние арифметические из процентных (долевых) соотношений, рассчитанных по одноименным периодам;

12, 13,14. Сетоды укрупнения интервалов, скользящй средней и аалитич выравн.

В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.

Выделяют три основных способа обработки динамического ряда:

а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;

б) метод скользящей средней;

в) аналитическое выравнивание (выравнивание по аналитическим формулам).

Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:

При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:

Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:

1) используя полусумму уровней, расположенных рядом с интерполируемыми;

2) по среднему абсолютному приросту;

3) по темпу роста.

Способ определения количественных значений за пределами ряда называют экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем.

Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.

При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле

Автокорреляцию в рядах можно устранить, коррелируя не сами уровни, а так называемые остаточные величины (разность эмпирических и теоретических уровней). В этом случае корреляцию между остаточными величинами можно определить по формуле

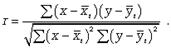
Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития.

При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период:

В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев:

15.Системы одновременных уравнений

Система одновременных уравнений — совокупность эконометрических уравнений (часто линейных), определяющих взаимозависимость экономических переменных. Важным отличительным признаком системы «одновременных» уравнений от прочих систем уравнений заключается в наличии одних и тех же переменных в правых и левых частях разных уравнений системы (речь идет о так называемой структурной форме модели, см. ниже).

Эндогенными называются переменные, значения которых определяются в процессе функционирования изучаемой экономической системы. Их значения определяются «одновременно» исходя из значений некоторых экзогенных переменных, значения которых определяются вне модели, задаются извне. В системах одновременных уравнений эндогенные переменные зависят как от экзогенных переменных, так и от эндогенных.

Измерение тесноты связи между переменными, построение изолированных уравнений регрессии недостаточно для объяснения функционирования сложных экономических систем. Изменение одной переменной не может происходить при абсолютной неизменности других. Её изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Таким образом отдельно взятое уравнение регрессии не может характеризовать истинное влияние отдельных признаков на вариацию результирующей переменной. Поэтому в экономических исследованиях важное место заняла проблема описания структуры связей между системой переменных.

труктурной формой системы называется представление системы, в котором в уравнениях может присутствовать более одной эндогенной переменной (в стандартной записи это означает, что в правой части уравнений, то есть в качестве регрессоров, имеются эндогенные переменные). Структурная форма системы описывает систему взаимозависимостей между экономическими переменными.

Перенеся эндогенные переменные в левую часть структурную форму можно представить в следующем матричном виде

Приведённой (прогнозной) формой системы называется представление системы, в котором в каждом уравнении имеется только одна эндогенная переменная, то есть эндогенные переменные выражены через экзогенные:

Это так называемая неограниченная приведённая форма. Структурную форму можно записать следующим образом:

Это так называемая ограниченная приведённая форма, то есть приведённая форма с ограничением на коэффициенты следующего вида: .

Если задана структурная форма, то всегда можно получить ограниченную приведённую форму (предполагается, что матрица А невырождена). Однако, обратное не всегда возможно, а если возможно, то не всегда однозначно.

Структурное уравнение называется идентифицируемым, если его коэффициенты можно выразить через коэффициенты приведённой формы. Если это можно сделать единственным способом, то говорят о точной индентифицируемости, если несколькими способами — о сверхидентифицируемости. В противном случае оно называется неидентифицируемым. Сверхидентифицируемость фактически означает, что на коэффициенты приведённой формы наложены некоторые ограничения (сверхидентифицирующие). В полной приведённой форме участвуют все экзогенные переменные и на коэффициенты не налагается никаких ограничений.

Необходимое условие идентифицируемости структурного уравнения (порядковое условие): количество переменных правой части уравнения должно быть не больше количества всех экзогенных переменных системы. В канонической форме (когда "левой" и "правой" частей нет) данное условие иногда формулируют следующим образом: количество исключенных из данного уравнения экзогенных переменных должно быть не меньше количества включенных эндогенных переменных уравнения минус единица. Если данное условие не выполнено, то уравнение неидентифицируемо. Если выполнено со знаком равенства, то, вероятно, точно идентифицируемо, иначе - сверхидентифицируема.

Достаточное условие идентифицируемости структурного уравнения: ранг матрицы, составленной из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении, не меньше общего числа эндогенных переменных системы минус единица.

16. Моделирование структурными уравнениями.

Моделирование Структурными Уравнениями

(structural equation modeling) Используемое при разработке множества проблем, от изучения академических достижений до исслед. динамики настроения, М. с. у. представляет собой систематический анализ причинных связей. Широкое применение М. с. у., наз. еще анализом спроса (demand analysis), многопараметрическим комплексным анализом (multitrait multimethod analysis), путевым анализом (path analysis), линейным причинным анализом (linear causal analysis) или методом одновременных уравнений (simultaneous equations), можно объяснить, в значительной степени, двумя отличительными особенностями исслед. в науках о поведении. Во-первых, поскольку мн. исслед. поведения не являются экспериментальными, анализ неэкспериментальных данных требует использования статистических процедур в качестве альтернатив эксперим. манипулированию и контролю. Цель статистических процедур, неразрывно связанных с М. с. у., - достичь уровня оценки, характерного для эксперим. исслед. Во-вторых, предметом мн. исслед. являются гипотетическиеконструкты, не доступные прямому наблюдению, но оказывающие решающее воздействие на измеряемые переменные и характер связей между ними. Поэтому были разработаны модели, учитывающие и латентный аспект этих переменных, и их эмпирическую связь с измеряемыми переменными. Уравнения регрессии дают информ. о степени эмпирической связи между изучаемыми переменными, представленную в форме утверждения "когда изменяется х, то изменяется и y". Структурные уравнения представляют более высокий уровень абстракции, на к-ром при данном эмпирическом объединении переменных в центре оказываются причинные связи. Несмотря на это различие, уравнения регрессии можно использовать для оценки структурных уравнений, если выполняется ряд условий. Во-первых, идентифицированные в данной модели причинные переменные не должны зависеть от др. неустановленных причин или, в противоположной формулировке, все существенные причинные переменные, связанные с изучаемым явлением, должны быть точно определены. Следовательно, М. с. у. требует высокой концептуальной (понятийной) и теорет. точности. Во-вторых, переменные, входящие в данную модель, являются либо дихотомическими, либо линейно взаимосвязанными. Линейные структурные модели можно эффективно использовать в исслед. нелинейных связей, если провести соотв. преобразования. В-третьих, причинные переменные либо измеряются без погрешности, либо предусматриваются эксплицитные процедуры для оценки ошибки измерения, как это имеет место при использовании многопараметрического комплексного анализа в моделях множественных индикаторов (multiple indicator models). В четвертых, направление и порядок причинных связей среди изучаемых переменных должны быть явно определены. Хотя это, возможно, не представляет особой проблемы в случае рекурсивной модели, моделирование реципрокной причинности требует использования более тонких и сложных аналитических процедур. Если эти четыре условия выполняются, тогда можно предложить причинную интерпретацию значений соотв. структурных коэффициентов. В науках о поведении крайне мало представляющих интерес явлений, к-рые поддаются адекватному описанию и анализу с т. зр. простой связи "причина -> следствие". Обычно поведенческие феномены встроены в сеть причинных отношений, что требует применения более мощных и точных аналитических процедур. Поскольку линейная регрессионная модель служит основой практически для всех статистических методов, используемых в поведенческих науках, в тех случаях, когда реальная и теорет. сложностьпревышает ограничения двумерной рекурсивной модели, в анализ могут вводиться др. линейные модели. Если целью анализа является идентификация множественных независимых переменных (предикторов), то можно применить модель множественной регрессии. Если, в дополнение к этому, приходится иметь дело с множественными зависимыми переменными, тогда можно воспользоваться многомерной регрессией. Наконец, если есть признаки реципрокных причинных связей между эндогенными переменными, тогда лучше всего использовать общую линейную модель структурных уравнений. В целях иллюстрации общей линейной модели структурных уравнений кратко рассмотрим пример из девяти переменных. Эти девять переменных разделяются на три характерные категории: эндогенные переменные, экзогенные переменные и возмущающие члены. Аналогично переменной У в двумерной модели, эндогенные переменные - это переменные, значения которых полностью определяются причинными связями, заданными в исследуемой модели. В нашем примере эндогенные переменные представлены переменными D, Е и F. Экзогенные переменные - А, В и С - это переменные, в отношении к-рых предполагается, что теоретически они могут оказывать заметное воздействие на эндогенные переменные, однако их значения определяются внешними процессами, не включенными на данный момент в рассматриваемую модель. Связанные с каждой эндогенной переменной возмущающие члены (и) показывают, какая доля изменчивости соотв. эндогенной переменной не объясняется др. переменными, входящими в данную модель. Как можно заметить на приведенной выше структурной схеме, ряд логически возможных причинных связей не определен (напр. А-Е, B-F, C-D). Эту причинную модель можно преобразовать в следующую систему из трех структурных уравнений: D = bDAА + bDВВ + uD, Е = bEBВ + bEDD + bEFF + uE, F = bFCC + bFEE + uF. Полученная система уравнений отображает структурную модель поведенческих и стохастических процессов, предположительно порождающих определенное множество данных. Хотя при использовании М. с. у. приходится решать целый ряд технических вопросов (напр. задачиидентификации модели и оценивания параметров), роль теории остается крайне важной. Несмотря на применение в анализе предполагаемых причинных связей строго установленных статистических методов, начальный импульс и главные ориентиры М. с. у. определяются взаимодействием теорет. и методологических соображений

17. Построение и Анализ целевых функций

Функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.

В широком смысле целевая функция есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим. Примером критерия в теории статистических решений является среднеквадратический критерий точностиаппроксимации. Цель – найти такие оценки, при которых целевая функция достигает минимума.

Важно, что критерий всегда привносится извне, и только после этого ищется правило решения, минимизирующее или максимизирующее целевую функцию.

Целевая функция начинается с установления миссии организации. Миссия обычно идентифицируется с философией организации и отвечает на вопросы: для чего создана организация, какую потребность она удовлетворяет, каковы принципы ее деятельности. На основе миссии вырабатываются цели. Цель – это конкретизация миссии в форме доступной для управления процессом ее реализации. Хорошо сформулированные цели должны быть: измеримы, достижимы (реальны), ориентированы на определенные интервалы времени, взаимосвязаны друг с другом, не противоречивы, адресны и контролируемы.

- Планирование. План – это решение относительно системы мероприятий, предусматривающей порядок, последовательность, сроки и средства выполнения этих мероприятий. Планирование включает: установление целей и задач, разработку стратегии, программ и планов для достижения целей, определение необходимых ресурсов и их распределение по целям и задачам, доведение планов до тех, кто их должен выполнять.

Стратегическое планирование определяет основные цели и направление действий организаций и обеспечивает достижение выбранных целей путем использования имеющихся преимуществ и создания новых. Процесс стратегическое планирования это цикл состоящий из этапов: миссия организации, цели организации, оценка и анализ внешней среды, управленческое обследование сильных и слабых сторон, анализ стратегических альтернатив, выбор стратегии, реализация стратегии, оценка стратегии.

Составной частью планирования является прогнозирование – научно обоснованная деятельность по составлению прогнозов. Прогноз – это вероятностное, научно обоснованное суждение о перспективах, возможных состояниях того или иного объекта в будущем и (или) об альтернативных путях и сроках достижения будущих состояний.

- Организация – функция управления, задачей которой является формирование структуры организации. Организовать – это значит разделить на части и делегировать выполнение общей управленческой задачи путем распределения ответственности и полномочий, а также установление взаимосвязей между различными видами работ.

- Мотивация – побуждение к эффективной деятельности людей, работающих в организации, ради достижения поставленных целей. Действия по мотивации включают в себя экономическое и моральное стимулирование, создание условий для проявления творческого потенциала работников и их саморазвития. В общем виде процесс мотивации включает: установление неудовлетворенных потребностей сотрудников, формулировку целей, направленных на удовлетворение потребностей.

- Контроль – управленческая функция, задачей которой является количественная и качественная оценка и учет результатов работы организации. В этой функции выделяются два основных направления: контроль за выполнением работ, намеченных планом и меры по коррекции всех значительных отклонений от плана. Главные инструменты выполнения этой функции – наблюдение, учет и анализ.

Координация – функция процесса управления, обеспечивающая его бесперебойность и непрерывность. Главная задача координации – достижение согласованности в работе, всех звеньев организации путем установления рациональных связей между ними.

18. Экстраполяция тенденции как метод прогнозирования

метод прогнозирования - экстраполяция статистических тенденций. Существует две разновидности такого метода:

- экстраполяция временных рядов

- определение скользящего среднего

Экстраполяция - это, проще говоря, продление тенденции. Есть два основных вида экстраполяции. Первый вид - линейная экстраполяция. Второй вид экстраполяции - криволинейная экстраполяция, т. е. продление тенденции по кривой. Это - криволинейная модификация линейной экстраполяции.

Существует множество статистических пакетов компьютерных программ, с помощью которых проводят экстраполяцию на основании имеющихся данных.

Прогнозирование с помощью скользящего среднего

По своей сути прогнозирование с помощью скользящего среднего есть осреднение подъемов и спадов сезонных колебаний, продленное в будущее. Цель экстраполяции - сглаживание колебаний. Рассмотрим пример. Кривая инфляции изменяется от месяца к месяцу, поэтому единственный путь выявить тенденцию - это сгладить колебания путем осреднения. После получения данных по каждому очередному месяцу они осредняются, скажем, по последним трем месяцам для получения скользящего среднего на четырехмесячный период.

Дата добавления: 2015-08-17