Читайте также:
|
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:
(5)
где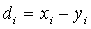 
— разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;
Sd вычисляется по следующей формуле:
(6)
Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок.
Если tэмп<tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
8. Множественная регрессия
Дата добавления: 2015-08-17; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| А) случай независимых выборок | | | Множественная регрессия |