S-кривая

S-образная форма экстраполяционной кривой применяется при прогнозах темпов замены одной технологии на другую или одного вида товара другим.

Однако метод S-кривой имеет определенные ограничения в применении. Вот одна из проблем. Хорошо известно, что данные ведут себя в форме S-кривой.

19. Балансовая модель анализа и планирования трудовых ресурсов.

аблица межотраслевых связей, построенная по такой схеме, отражает структуру затрат на произ-во каждого продукта и структуру его распределения в нар. хозяйстве. Цифры по вертикали (направление линии А) характеризуют состав продукции каждой отрасли по стоимости. Здесь отражаются как материальные ресурсы, полученные от др. отраслей,так и затраты живого труда в форме зарплаты и прибавочного продукта, а также амортизационные отчисления. По горизонтали (направление линии Б) приведены данные о том,на какую сумму или какое количество продукции передано из данной отрасли в др. отрасли нар. х-ва на производств. нужды (промежуточныйпродукт), а также конечное потребление продукции на цели личного и обществ. потребления и накопления,возмещение и капитальный ремонт осн. фондов и экспортно-импортное сальдо (распределение продукции и стоимости).

По экономич. содержанию и характеру информации можно выделить 2 осн. разновидности балансов: стоимостный и натурально-продуктовый; каждый из них,в свою очередь, может быть отчётным или плановым. Отчётные Б. м. разработаны ЦСУ СССР за 1959 и 1966. Наряду с балансами, охватывающими все отрасли нар. х-ва СССР, разрабатываются региональные модели по отд. союзным республикам и экономич. р-нам. Стоимостные Б. м. характеризуют процесс воспроизводства в ден. выражении. Балансы этого типа охватывают все 4 квадранта принципиальной схемы. По своей структуре стоимостные Б. м. могут быть укрупнёнными или детальными. Б. м. в натуральном выражении разрабатываются по конкретным видам продукции (по видам проката, важнейшим хим. продуктам,осн. разновидностям машин и т. д.).

Количественная взаимосвязь между отраслями х-ва математически в элементарном виде может быть 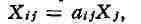представлена формулой:

где a_ij - количество продукции одной отрасли i, необходимое для произ-ва единицы продукции другой отрасли j (напр., количество условного топлива на выработку тепловыми электростанциями 1 квт-ч электрич. энергии); Xj - объём продукции, к-рый должен быть произведён потребляющей отраслью j (напр., количество электрич. энергии в квтч, к-рое должно быть выработано всеми тепловыми электростанциями); Xjj показывает весь поток отрасли " в отрасль j. Затраты продукции одной отрасли на произ-во единицы продукции другой отрасли наз. коэфф. прямых затрат.

Модель статич. Б. м. может быть представлена след. системой линейных ур-ний:

где Y характеризует размер конечного потребления данной отрасли вар. х-ва.

Для анализа межотраслевых связей, эффективности структурных сдвигов в материальном произ-ве и осуществления плановых расчётов по системе межотраслевого баланса исчисляются также коэфф. полных затрат, характеризующие затраты к.-л. продукта на произ-во единицы другого продукта по всей цепи взаимосвязанных отраслей. Так, напр., полные затраты электроэнергии на производство 1 т алюминия складываются не только из расхода электроэнергии непосредственно на электролиз и на произ-во глинозёма, криолита, но также из расхода электроэнергии на произ-во материалов, поступающих из других отраслей пром-сти, в частности химикатов,топлива и т. п. Коэфф. полных затрат находятся решением указанной выше системы алгебраич. ур-ний. Расчёт коэфф. полных затрат связан с громадной вычислит. работой. Поэтому проведение таких расчётов практически стало возможно лишь при использовании электронно-вычислит. техники.

Разработка плановых Б. м. может осуществляться также на основе динамич. моделей. Динамич. модель представляет собой систему линейных ур-ний, обеспечивающих взаимную увязку показателей произ-ва, объёма капитальных вложений и трудовых ресурсов.

Исследования межотраслевых связей с помощью балансовых таблиц открыли возможности более глубокого изучения процессов социалистич. воспроизводства. На основе Б. м. можно глубже изучать основные закономерности социалистич. х-ва, соотношение развития обществ. продукта и нац. дохода, I и II подразделений общественного производства, взаимосвязи произведённого и использованного нац. дохода, взаимосвязи между пром-стыо, с. х-вом, строительством, отраслями сферы обращения. Метод Б. м. используется при исследовании методо-логич. проблем ценообразования и в практике пересмотра оптовых цен. На основе Б. м. производятся расчёты структуры и уровня цен при различных концепциях ценообразования.

Коэфф. полных затрат,определённые на основе Б. м.,находят всё большее применение для решения проблем рационального междунар. разделения труда, расчётов эффективности внешней торговли, а также для междунар. сопоставлений уровня экономич. развития стра

Запишем матрицу прямых затрат соответственно данному варианту:

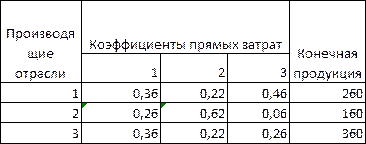
Также посчитаем затраты живого труда:

Единичная матрица:

Производ. Отрасли	Коэффициенты полных материальных затрат	Затраты труда на конечную продукцию	Затраты труда по отраслям
	aj*tj	Yj*tj	T
tj		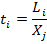Х	Х
Tj		Х	Х

20.Макроэкономическаямодель Менгеса

Модель Менгеса:

Yt = a1 + b11 ⋅ Yt −1 + b12 ⋅ I t + ε 1;

I t = a 2 + b21 ⋅ Yt + b22 ⋅ Qt + ε 2;

C t = a 3 + b31 ⋅ Yt + b32 ⋅ C t −1 + b33 ⋅ Pt + ε 3;

Qt = a 4 + b41 ⋅ Qt −1 + b42 ⋅ Rt + ε 4,

где Y– национальный доход;

С – расходы на личное потребление;

I – чистые инвестиции;

Q – валовая прибыль экономики;

1. Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели.

2. Запишите, если возможно, приведенную форму модели.

Вариант 1. Модель Менгеса:

где Y - национальный доход;

С - расходы на личное потребление;

I - чистые инвестиции;

Q - валовая прибыль экономики;

Р - индекс стоимости жизни;

R - объем продукции промышленности;

t - текущий период;

t-1 - предыдущий период.

Дата добавления: 2015-08-17