Модель экономического роста Харрода

Исследования Домара на несколько лет предвосхитила ставшая теперь знаменитой модель экономического роста Харрода. ² Последний сосредоточил свое внимание на четкой формулировке в явном виде условий равновесия намечаемых сбережений и инвестиций в расширяющейся экономике. Модель Харрода, основанная на принципе акселерации, к тому же отражала положения теории инвестиционного спроса. В анализе Харрода равновесие сбережений и инвестиций должно рассматриваться в общем контексте экономического роста потому, что, во-первых, сбережения являются функцией от уровня дохода и, во-вторых, капиталовложения (в силу принципа акселерации инвестиционного спроса) представляют собой - по крайней мере частично - функцию от прироста дохода. Но если условием осуществления инвестиций служит увеличение дохода, то вслед за повышением дохода будут расти и сбережения. Следовательно, поддержание равновесия между (намечаемыми) сбережениями и инвестициями требует также увеличения инвестиций. Проблема заключается в следующем: как определить темп роста, способный обеспечить указанное равенство.

Решение проблемы можно начать с использования традиционного условия макроэкономического равновесия:

S = I. (6)

Кроме того, предполагается, что сбережения (S) представляют собой постоянную долю (s) дохода, т. е.:

S =sY, 0 < s < l, (7)

где, как и раньше, символа используется для обозначения постоянной средней (а следовательно, и предельной) склонности к сбережению. В соответствии с принципом акселерации полагаем, что инвестиции составляют постоянную долю в приросте продукции

I = αΔY, (8), где ΔY=Y(t)-Y(t-1).

где α представляет собой коэффициент акселерации, ΔK/ΔY - определяемый техническими факторами предельный капитальный коэффициент. Подстановка (7) и (8) в соотношение (6) позволяет перейти к следующему выражению:

sY = αΔY. (9)

Разделив обе части равенства (9) на α и Y, мы можем определить темпы роста национального дохода:

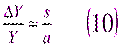или

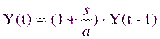
Его решение имеет вид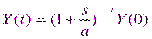

Таким образом, условием постоянного сохранения равенства между намечаемыми сбережениями и инвестициями служит постоянный темп увеличения национального продукта, равный s/α. Например, при s = 0,12 и α = 3 темп равновесного экономического роста составит 4% в год. Заметим, что равновесный темп роста будет менять свою величину в том же направлении, что и s, и в обратном изменению α. В рамках данной модели такие соотношения представляются довольно естественными. Чем большая доля дохода сберегается, тем больше должен быть и темп роста национального продукта, чтобы механизм акселерации вызвал к жизни инвестиции, достаточные для поглощения планируемых сбережений. Аналогично, чем меньше акселератор α, тем меньше инвестиции, индуцируемые заданным увеличением национального продукта, а следовательно, тем выше темп экономического роста, требуемый для поглощения данной суммы сбережений.

25.Модельадаптивныхожиданий

Динамической эконометрической моделью называется модель, которая в настоящий момент времени учитывает значения входящих в неё переменных, относящихся не только к текущему, но и к предыдущему моментам времени.

В качестве примера динамических эконометрических моделей можно привести модели вида:

yt=f(xt,xt–l),

yt=f(xt,yt–l).

Модель регрессии вида:

yt=f(x1…xn)=f(xi) не относится к динамическим эконометрическим моделям.

Моделью адаптивных ожиданий называется динамическая эконометрическая модель, которая учитывает предполагаемое или желаемое значение факторной переменной

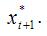
Общий вид модели адаптивных ожиданий:

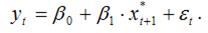
Примером модели адаптивных ожиданий является модель зависимости предполагаемой в будущем периоде (t+1) индексации заработных плат и пенсий на текущие цены.

косвенный метод адаптивных ожиданий . Этот метод использует корректировку ожиданий. В каждый момент времени реальное значение переменной сравнивается с ее ожидаемым значением. Если реальное значение оказывается больше, то значение, ожидаемое в следующий момент (период), корректируется в сторону повышения, если меньше — в сторону уменьшения. Размер корректировки пропорционален разности между реальным и ожидаемым значением переменной.

Если распределение Койка и основанный на нем метод моделирования ожиданий основываются на предположении, что коэффициенты при лаговых объясняющих переменных убывают в геометрической прогрессии, то такое предположение выполняется далеко не всегда. Поэтому в некоторых случаях эти методы используются обоснованно и приводят к правильным результатам. А в других ситуациях их применение необоснованно и может приводить к неверным результатам, да и сама реализация их оказывается затруднительной.

Так, во многих случаях значительно более уместно предположить, что изменение зависимой переменной в ответ на изменение объясняющей переменной сначала невелико, а затем, с течением времени оно возрастает, а по прохождении некоторого периода такого возрастания — опять уменьшается.

Моделирование такого поведения с использованием минимального числа параметров предлагает метод распределенных лагов Алмон . Метод лагов Алмон обладает достаточной гибкостью, он удобен в применении и достаточно эффективно справляется с вычислительными трудностями и спецификой различных зависимостей. Центральная идея этого метода заключается в следующем. Предполагается, что если зависимое переменное у характеризуется зависимостью от текущих и лаговых значений объясняющей переменной х, то веса в этой зависимости подчиняются полиномиальному распределению. Именно поэтому лаги Алмон часто описываются как полиномиально распределенные лаги. Сам выбор конкретного полинома (прежде всего, его степень) определяется исследователем на основе экспериментов.

Далее выбирается число лаговых значений объясняющей переменной , которое опять же находится в результате экспериментов, направленных на получение информации, необходимой для хорошего описания данных и соответствующего моделирования таких данных. К сожалению, на практике распределение лагов объясняющей переменной может плохо поддаваться аппроксимации с помощью более простых функций. Так, сама автор данного метода Алмон использовала полином четвертой степени и получила вполне хорошие результаты. Но дело в том, что с ростом степени полиномов увеличивается риск появления неучтенной мультиколлинеарности.

Более того, дефектом адаптивных ожиданий и иных похожих способов учета ожиданий является то, что получаемые с их помощью прогнозы в общем случае отличаются от прогнозов, получаемых с помощью модели в целом. Для преодоления подобных недостатков служат методы рациональных ожиданий. Проще всего представить, что основное в рациональных ожиданиях это допущение, что экономические агенты имеют доступ ко всей адекватной информации и что они наилучшим образом ее используют при формировании ожиданий относительно будущих значений экономических переменных.

26.Проби-илогит-анализ

---

Дата добавления: 2015-08-17