А) случай независимых выборок

Статистика критерия для случая несвязанных, независимых выборок равна:

(1)

где 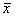, — средние арифметические в эксперименталь­ной и контрольной группах,

- стан­дартная ошибка разности средних арифметических. Находится из формулы:

, (2)

где n₁ и n₂ соответственно величины первой и второй выборки.

Если n₁=n₂, то стандартная ошибка разности средних арифметических будет считаться по формуле:

(3)

где n величина выборки.

Подсчет числа степеней свободы осуществля­ется по формуле:

k = n₁ + n₂ – 2. (4)

При численном равенстве выборок k = 2n - 2.

Далее необходимо срав­нить полученное значение t_эмп с теоретическим значением t—рас­пределения Стьюдента (см. приложение к учеб­никам статистики). Если t_эмп<t_крит, то гипотеза H₀ принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.

Дата добавления: 2015-08-17