Линейный коэффициент корреляции

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле^[10][8]:

5. Криетрий Фишера

F-тестом или критерием Фишера (F-критерием, φ*-критерием) — называют любой статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение).

Статистика теста так или иначе сводится к отношению выборочных дисперсий (сумм квадратов, деленных на "степени свободы"). Чтобы статистика имела распределение Фишера необходимо, чтобы числитель и знаменатель были независимыми случайными величинами и соответствующие суммы квадратов имели распределение Хи-квадрат. Для этого требуется, чтобы данные имели нормальное распределение. Кроме того, предполагается, что дисперсия случайных величин, квадраты которых суммируются, одинакова.

Тест проводится путем сравнения значения статистики с критическим значением соответствующего распределения Фишера при заданном уровне значимости. Известно, что если , то . Кроме того, квантили распределения Фишера обладают свойством . Поэтому обычно на практике в числителе участвует потенциально большая величина, в знаменателе - меньшая и сравнение осуществляется с "правой" квантилью распределения. Тем не менее тест может быть и двусторонним и односторонним. В первом случае при уровне значимости используется квантиль , а при одностороннем тесте ^[1].

Более удобный способ проверки гипотез - с помощью p-значения 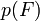- вероятностью того, что случайная величина с данным распределением Фишера превысит данное значение статистики. Если 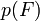(для двустороннего теста - )) меньше уровня значимости , то нулевая гипотеза отвергается, в противном случае принимается.

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух независимых выборок. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фи­шера такова:

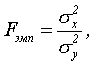(8)

где - дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмпвсегда будет больше или равно единице.

Чис­ло степеней свободы определяется также просто:

k₁=n_l - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k₂=n₂ - 1 для второй выборки.

t_эмп>t_крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная

Дата добавления: 2015-08-17