
|
Читайте также: |
Дифракцией света называют огибание лучами света контура непрозрачных тел, соизмеримых с длиной волны изучения, и проникновение света в область геометрической тени.
Явление дифракции объясняется принципами Гюйгенса и Гюйгенса – Френеля.
 Согласно принципу голландского физика Гюйгенса, зная положение фронта волны в момент времени
Согласно принципу голландского физика Гюйгенса, зная положение фронта волны в момент времени  и скорость движения волны υ можно определить положение фронта волны в момент времени
и скорость движения волны υ можно определить положение фронта волны в момент времени 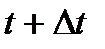 .
.
| Рис. 1 |
 фронт волны представлен в виде поверхности
фронт волны представлен в виде поверхности  . Согласно принципу Гюйгенса все точки этой поверхности являются источниками вторичных волн. При этом принимается, что в однородной среде вторичные волны - сферические и излучаются только вперед. Огибающая всех вторичных волн даст положение фронта волны через время
. Согласно принципу Гюйгенса все точки этой поверхности являются источниками вторичных волн. При этом принимается, что в однородной среде вторичные волны - сферические и излучаются только вперед. Огибающая всех вторичных волн даст положение фронта волны через время  , то есть
, то есть 
Принцип Гюйгенса позволяет объяснить проникновение световых волн в область геометрической тени, но не дает сведений об интенсивности волн, распространяющихся в различных направлениях.
Решение этой задачи предложил французский физик Френель О.Ж., положив, что все вторичные источники являются когерентными и могут интерферировать. Разработанный Френелем приближенный метод решения задач о распространении волн (особенно световых) впоследствии был назван принципом Гюйгенса-Френеля.
Принцип Гюйгенса-Френеля определяется следующими положениями:
а) Источник  (рис.2) заменяется эквивалентной ему системой вторичных источников
(рис.2) заменяется эквивалентной ему системой вторичных источников  - участков волновой поверхности
- участков волновой поверхности  , охватывающей
, охватывающей  ;
;
б) Вторичные источники когерентны между собой и поэтому интерферируют. Так как  волновая поверхность
волновая поверхность  , то фазы колебаний вторичных источников одинаковые;
, то фазы колебаний вторичных источников одинаковые;
в) Амплитуда  колебаний, возбуждаемых в точке М вторичным источником
колебаний, возбуждаемых в точке М вторичным источником  ,
,
 , (1)
, (1)

|
где  - величина, определяемая амплитудой светового колебания в
- величина, определяемая амплитудой светового колебания в  ;
;  - функция угла
- функция угла  , монотонно убывающая от 1 при
, монотонно убывающая от 1 при  =0 до при
=0 до при  (т.к. вторичные источники не излучают назад).
(т.к. вторичные источники не излучают назад).
г) Если часть поверхности  закрыть непрозрачным экраном, то закрытые вторичные источники не излучают, а остальные излучают так же, как и в отсутствие экрана. С помощью принципа Гюйгенса-Френеля обосновывается с волновой точки зрения закон прямолинейного распространения света в однородной среде. Пусть
закрыть непрозрачным экраном, то закрытые вторичные источники не излучают, а остальные излучают так же, как и в отсутствие экрана. С помощью принципа Гюйгенса-Френеля обосновывается с волновой точки зрения закон прямолинейного распространения света в однородной среде. Пусть  - точечный источник монохроматического (
- точечный источник монохроматического ( ) света, а М - точка наблюдения,
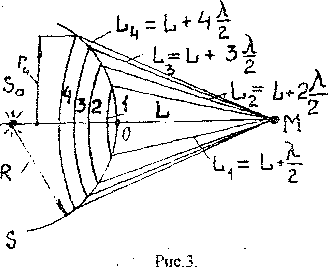
) света, а М - точка наблюдения,  - вспомогательная волновая поверхность радиусом
- вспомогательная волновая поверхность радиусом  (рис.3). Принимается
(рис.3). Принимается 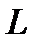 порядка
порядка  .
.
|
Поверхность разбивается на кольцевые участки так, чтобы расстояние от края каждой зоны до М отличалось на 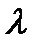 /2. Такие участки называют зонами Френеля. Первая зона возбуждает в точке М колебания с амплитудой А1, вторая зона – А2, третья – А3 и т.д.
/2. Такие участки называют зонами Френеля. Первая зона возбуждает в точке М колебания с амплитудой А1, вторая зона – А2, третья – А3 и т.д.
Колебания, возбуждаемые в точке М двумя соседними зонами, противоположны по фазе, т.к. разность хода равна  /2. Следовательно, амплитуда результирующих колебаний в точке М
/2. Следовательно, амплитуда результирующих колебаний в точке М
А =А1 - А2 + А3 – А4 +.... (2)
Амплитуда А i колебаний, возбуждаемых i -той зоной согласно формулы (1) зависит от площади зоны  i, угла
i, угла  i и расстояния
i и расстояния  i.
i.
Путем относительно простого вывода установлено, что площади зон Френеля равны. При этом для небольшого числа зон получают формулу для определения радиуса внешней границы зоны в виде
 . (3)
. (3)
Если положить  =
=  =1 м,
=1 м,  = 0,5 мкм и i =1, то
= 0,5 мкм и i =1, то  0,5 мм. Радиусы последующих зон возрастают пропорционально
0,5 мм. Радиусы последующих зон возрастают пропорционально  . С ростом i расстояние
. С ростом i расстояние  i и угол
i и угол  i увеличиваются монотонно. Это приводит к тому, что амплитуда А i, колебания возбуждаемого i -той зоной в точке М, монотонно убывает с ростом i. Следовательно,
i увеличиваются монотонно. Это приводит к тому, что амплитуда А i, колебания возбуждаемого i -той зоной в точке М, монотонно убывает с ростом i. Следовательно,
A1>A2>A3>A4……….
В пределах небольших i зависимость А i от i является практически линейной
 . (4)
. (4)
Запишем выражение (2) в виде
 (5)
(5)
С учетом формулы (4), выражения в скобках получаются равными нулю. Поэтому
 . (6)
. (6)
Следовательно, амплитуда колебаний, создаваемая в точке М всей сферической волновой поверхностью  , равна половине амплитуды, создаваемой одной лишь первой (центральной) зоной. Колебания от остальных зон взаимно компенсируются.
, равна половине амплитуды, создаваемой одной лишь первой (центральной) зоной. Колебания от остальных зон взаимно компенсируются.
Различают два случая дифракции света: дифракцию Френеля, или дифракцию в сходящихся лучах, и дифракцию Фраунгофера, или дифракцию в параллельных лучах.
В простейших случаях дифракции Френеля вид дифракционной картины можно объяснить методом зон Френеля.
Рассмотрим явление дифракции света и дифракционную картину от круглого препятствия.
Поместим между точечным источником света  и точкой наблюдения на экране М непрозрачный диск радиусом
и точкой наблюдения на экране М непрозрачный диск радиусом  (рис.4).
(рис.4).
Если диск закроет m первых зон Френеля, то в точке М


Рис.4
Полагая выражения в скобках равными нулю, получают
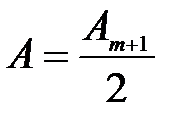 (7)
(7)
Значит, в точке М всегда находится интерференционный максимум. Далее следуют чередующиеся темные и светлые кольца. По мере увеличения отношения  яркость светлого пятна постепенно уменьшается, а следующее за ним темное кольцо расширяется, образуя за диском тень.
яркость светлого пятна постепенно уменьшается, а следующее за ним темное кольцо расширяется, образуя за диском тень.
ПРАКТИЧЕСКАЯ ЧАСТЬ
ЛАБОРАТОРНАЯ УСТАНОВКА
Лабораторная установка состоит из оптической скамьи и закрепленных на стойках лазера, рамки с натянутой проволокой и экрана.
Луч света полупроводникового лазера диаметром 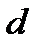 = 2 мм направляется на вертикально натянутую проволоку и далее на экран Э (рис. 5).
= 2 мм направляется на вертикально натянутую проволоку и далее на экран Э (рис. 5).

Рис. 5.
При определенном соотношении 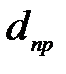 , L1 и L на экране наблюдается дифракционная картина, состоящая из чередующихся светлых и темных полос.
, L1 и L на экране наблюдается дифракционная картина, состоящая из чередующихся светлых и темных полос.
Согласно теории, изложенной ранее, в центре (точка С) будет находиться светлая полоса (интерференционный максимум), так как лучи АС и БС равны.
На соседних участках (например, в точке Е) наличие интерференционного максимума или минимума определяется разностью хода лучей АЕ и ДЕ, то есть отрезком БД.
Если БД = 2  , (8) n = 0, 1, 2, 3,...(разностъ хода лучей равна четному числу полуволн), то в точке Е будет интерференционный максимум (светлая полоса).
, (8) n = 0, 1, 2, 3,...(разностъ хода лучей равна четному числу полуволн), то в точке Е будет интерференционный максимум (светлая полоса).
При БД = (2 n - 1)  , (9) (разность хода лучей равна нечетному числу полуволн) в точке Е наблюдается интерференционный минимум (темный участок).
, (9) (разность хода лучей равна нечетному числу полуволн) в точке Е наблюдается интерференционный минимум (темный участок).
На рис. 5 изображена интерференционная картина, наблюдаемая на экране. Расстояния между серединами соседних светлых или темных участков h равны длине волны  , что следует из формулы (8) и (9).
, что следует из формулы (8) и (9).
В точке С, как показано ранее, наблюдается светлый участок - нулевой максимум. Пусть в точке Е будет следующий светлый участок - первый максимум. Следовательно, при n = 1 из формулы (8) следует, что отрезок  .
.
Треугольники ОСЕ и АБД подобны. Отсюда
 ;
;  и окончательно
и окончательно  . (10)
. (10)
Таким образом, измерив диаметр проволоки  , расстояние
, расстояние  между проволокой и экраном и расстояние между соседними максимумами или минимумами освещенности на интерференционной картине, по формуле (10) можно рассчитать длину волны света.
между проволокой и экраном и расстояние между соседними максимумами или минимумами освещенности на интерференционной картине, по формуле (10) можно рассчитать длину волны света.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. После изучения теоретической части ознакомиться с лабораторной установкой.
2. Установить расстояния между лазером и проволокой  1 = 150... 160 мм, между проволокой и экраном
1 = 150... 160 мм, между проволокой и экраном  = 680... 700 мм.
= 680... 700 мм.
3. Включить лазер и получить четкую интерференционную картину.
4. По миллиметровой бумаге определить расстояния h справа и слева от пятна луча. Удобнее измерять расстояние между темными участками. Результаты измерений занести в таблицу
| № измерения | |||||
| h, мм |
5. Обработать результаты измерений h по методике прямых измерений и записать результат.
6. Измерить диаметр проволоки  =0,07 мм.
=0,07 мм.
7. Измерить расстояние  от проволоки до экрана.
от проволоки до экрана.
8. Рассчитать длину волны излучения лазера.
9. Оценить относительную погрешность определения длины  .
.
СОДЕРЖАНИЕ ОТЧЕТА
Отчет по лабораторной работе должен содержать:
1. Краткую теоретическую часть, поясняющую явление дифракции света, принципы Гюйгенса и Гюйгенса — Френеля, метод зон Френеля, дифракционную картину от диска.
2. Схему лабораторной установки, схему хода лучей.
3. Интерференционную картину, полученную на экране.
4. Таблицу.
5. Результаты обработки данных по измерению h.
6. Результаты измерений  и
и  .
.
7. Расчет длины волны излучения лазера.
8. Оценка относительной погрешности определения длины волны  .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определение явления дифракции света.
2. Принципы Гюйгенса и Гюйгенса - Френеля.
3. Метод зон Френеля.
4. Дифракция от круглого диска.
5. Дифракция от проволоки. Условия максимумов и минимумов освещенности на интерференционной картине.
6. Порядок выполнения эксперимента.
7. Методика обработки результатов прямого измерения.
ЛИТЕРАТУРА
1. Трофимова Т.И. Курс физики. М.: Высшая школа. 1999. 542 с.
2. Детлаф Л.А.. Яворский Б.М Курс физики. М.гВыстдая школа. 2000. 718с.
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. Туполева
Кафедра технической физики
Дата добавления: 2015-08-02; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЗАКОНЫ ОСВЕЩЕННОСТИ | | | КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ |