Читайте также:
|
Если бегущая в среде волна, описываемая уравнением (2), достигает границы с более плотной средой, то она,изменяя фазу на 180°, отражается. На рис.5 жирной линией показана бегущая падающая волна, пунктиром - бегущая отраженная волна.
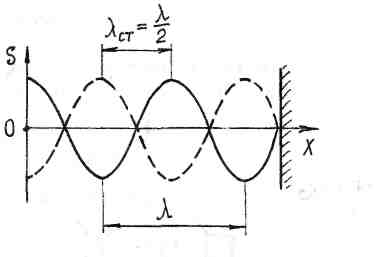
Рис.5
При сложении падающей и отраженной волн образуется так называемая стоячая волна.
Стоячая волна кажется неподвижной. Стоячие волны образуются при сложении двух гармонических бегущих навстречу друг другу волн с равными частотами и амплитудами, а для поперечных волн - и одинаковой поляризации.
Уравнение стоячей волны имеет вид:
(3)
где λ - длина бегущей волны (падающей и отраженной).
Величина 
называется амплитудой стоячей волны.
Она изменяется о т 0 до 2А. Амплитуда стоячей волны не зависит от времени и определяется координатой х. Точки, в которых амплитуда максимальна, называются пучностями. Для пучностей 
, что наблюдается при
где m=0,1,2, 3,...
Следовательно, координаты пучностей, отсчитываемые от места возбуждения, будут определяться как
, (4)
Точки стоячей волны, где амплитуда равна нулю, называются узлами. В
узлах 
. Следовательно,
координаты узлов
Пучности, как и узлы, располагаются друг от друга на расстояниях 
/2. Эту величину называют длиной стоячей волны
λст= λ/2.
Таким образом, длина стоячей волны равна половине длины бегущей
волны.
Дата добавления: 2015-08-02; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Упругие волны и их характеристики | | | Стоячие волны в трубе |