Теоретическая часть. Рассмотрим электрический колебательный контур (рис

Рассмотрим электрический колебательный контур (рис. 1) с последовательно

соединенным конденсатором емкостью С с катушкой индуктивности L и резистором сопротивления R. Сопротивление R является условно суммарным и включает в себя активное сопротивление катушки индуктивности, соединительных проводов и резистора. Эти сопротивления называются активными (или омическими), так как они потребляют электрическую энергию, идущую на увеличение их внутренней энергии, то есть нагрев.

Для колебательного контура энергия, потребляемая активными сопротивлениями, является потерей энергии.

В положении I переключателя К конденсатор заряжается от источника постоянного тока до напряжения U_C. При этом конденсатор получит заряд q и энергию

, (1)

называемую электрической энергией колебательного контура.

Переведем переключатель К в положение 2. Конденсатор начнет разряжаться и в цепи потечет электрический ток I. В катушке индуктивности L возникает магнитное поле и ЭДС самоиндукции

, (2)

противодействующая нарастанию тока.

По мере разряда конденсатора энергия электрического поля уменьшается, но одновременно увеличивается энергия магнитного поля

. (3)

При полной разрядке конденсатора ( =0, =0) =0.

Энергия магнитного поля согласно закону сохранению энергии станет максимальной. Следовательно, сила тока достигнет максимального значения , а ЭДС самоиндукции =0.

Далее магнитное поле катушки начнет уменьшаться из-за отсутствия тока его поддерживающего, станет уменьшаться и ток I. Возникшая вновь ЭДС самоиндукции будет уже поддерживать ток. В результате конденсатор перезарядиться. Далее процесс вновь повторяется.

Таким образом, заряд конденсатора , напряжение на конденсаторе , сила тока в контуре , а, следовательно, и падение напряжения на активном сопротивлении 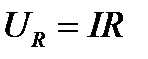будут периодически изменяться. В идеальном электрическом колебательном контуре без активного сопротивления ( =0) колебательный процесс совершается бесконечно долго. В реальном электрическом контуре, имеющем активное сопротивление (R>0) и соответствующие потери электрической энергии, колебания постепенно затухают.

Рассмотренные электромагнитные колебания аналогичны механическим колебаниям, например, колебаниям маятника, самоиндукция играет роль инерции, активное сопротивление – роль механического сопротивления. При колебаниях маятника потенциальная энергия отклоненного маятника переходит в кинетическую энергию движения и обратно. В электрическом колебательном контуре электрическая (потенциальная) энергия конденсатора переходит в энергию магнитного поля катушки, то есть «кинетическую» энергию тока и обратно.

Выведем уравнение колебаний заряда конденсатора в электрическом колебательном контуре с активным сопротивлением.

Согласно второму правилу Кирхгофа для произвольного момента времени

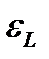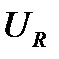+ + =0. (4)

Учитывая выражение (2) и что , , и противоположны по знаку, получают дифференциальное уравнение

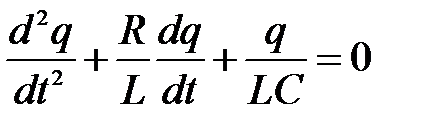(5)

Вводя обозначения

(6)

и

(7)

уравнение (5) записываем в виде

, (8)

где 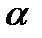- коэффициент, ω₀ - частота собственных колебаний электрического контура при =0.

Уравнение (8) имеет несколько решений в зависимости от соотношения коэффициентов и ω₀.

При , ,

(контур с малыми потерями) решение уравнения (8) имеет вид

, (9)

где - основание натуральных логарифмов, - начальная фаза,

круговая частота колебаний

, (10)

Разделив на С левую и правую части выражения (9), получают соотношение характеризующее изменение напряжения на конденсаторе

. (11)

Для силы тока в контуре соответственно записывают

. (12)

где амплитудное значение силы тока

, (13)

Величину в знаменателе называют «волновым» сопротивлением контура и обозначают

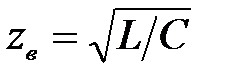. (14)

Графики зависимостей = , = , = изображаются в виде «затухающей» синусоиды (рис. 2) с постепенно убывающей амплитудой.

Таким образом, в колебательном контуре происходят колебания величин , , с круговой частотой , определяемой по формуле (10), условным периодом и амплитудами

, , ,

Коэффициент характеризует меру затухания и называется коэффициентом затухания.

Если , то есть 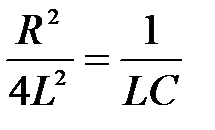, , то по формуле (10) ω=0 и . Следовательно, колебательный процесс в контуре исчезает и будет наблюдаться процесс апериодического разряда конденсатора. Решением уравнения (8) в этом случае является убывающая экспонента.

Режим, при котором колебательный процесс переходит в апериодический, называется критическим и характеризуется критическим сопротивлением

(15)

При , > _кр (режим с большими потерями) решением уравнения (8) будет также убывающая экспонента, характеризующая апериодический разряд конденсатора.

Рассмотренные решения наглядно представляют графически (рис. 3).

Для характеристики колебательного процесса вводят параметры: логарифмический декремент затухания и добротность .

Логарифмический декремент затухания равен натуральному логарифму отношения двух последовательных амплитуд А в одну сторону

. (16)

Отношение амплитуд называют декрементом затухания колебаний.

Добротность контура пропорциональна отношению запасенной в контуре энергии к ее потерям за период.

При слабом затухании

, (17)

то есть, добротность контура равна отношению волнового и активного сопротивлений.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Описание установки

Лабораторная установка состоит из лабораторного устройства, содержащего колебательный контур (рис. 1) и систем его питания, а также подключенного к нему осциллографа. Установка работает в двух режимах: затухающих и вынужденных колебаний.

В режиме затуханий колебаний на конденсатор колебательного контура напряжение подается импульсами. Во время действия импульса конденсатор заряжается. За время паузы между импульсами конденсатор разряжается и в контуре наблюдается колебательный процесс. На экран осциллографа выведены колебания .

В режимах вынужденных колебаний электрический колебательный контур питается от генератора, имеющегося в устройстве.

На передней панели устройства выведены следующие органы управления:

- «Сеть» - тумблер включения сети;

- «Режим» - тумблер режима работы устройства;

- «Затух» - затухающие колебания;

- «Вынужд» - вынужденные колебания;

- Тумблер переключения емкости контура С =0,05 и 0,1 мкФ;

- Тумблер переключения индуктивности контура L =0,5 и 1,0 Гн;

- Ручка R – изменения активного сопротивления в цепи контура;

- Ручка управления частотой f внутреннего генератора при работе в режиме вынужденных колебаний (от 100 Гц до 5 кГц);

- Гнездо «Осцил» - подключение осциллографа.

Подготовка к работе

1. Ознакомиться с теоретической частью и лабораторным устройством.

2. Установить тумблер режима в положение «Затух».

3. Ручку R поставить на наименьшее значение сопротивления.

4. Тумблеры C и L поставить в произвольное положение.

5. Включить лабораторное устройство и осциллограф в сеть.

6. Включить лабораторное устройство и осциллограф тумблерами «Сеть» и «Питание». Прогреть их в течение 2-3-х минут.

7. Получить устойчивую картину колебаний, регулируя ручками осциллографа (например, для осциллографа С1-73 ручками «Развертка», «Стаб», «Уровень», ).

Выполнение работы

1. Для установленных значений C и L рассчитать критическое сопротивление контура R_кр.

2. Установить минимальное сопротивление R₁ < R_кр.

3. Наблюдать и зарисовать картину колебаний.

4. Измерить период колебаний. Выполнить три измерения.

Таблица 1

Период колебаний, мс
Т1	Т2	Т3	Тэ

5. Измерить 4-5 последовательных или отрицательных амплитуд колебаний и записать их в таблицу 2

Таблица 2

Амплитуда в делениях шкалы	Отношение амплитуд (декремент)
U1	U2	U3	U4	U5	U1/U2	U2/U3	U3/U4	U4/U5	Среднее значение

6. Рассчитать среднее арифметическое значение периода колебаний Т_э (табл. 1) и декремента (табл. 2). *

7. По экспериментальным значениям Т_э и декремента определить параметры колебательного процесса контура: логарифмический декремент , коэффициент затухания и добротность контура . Значения занести в табл. 3.

8. Для данных L, C и R₁ рассчитать параметры колебательного процесса и контура α_р, Т_р, δ_р, Q_р (табл. 3)

R_{1 =} Таблица 3

Параметр		Т		Q
Единица измерения
Эксперимент
Расчет
Абсолютная погрешность
Относительная погрешность

9. Экспериментальным путем определить , , , 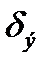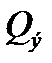для сопротивлений R₂ и R₃ при R₁<R₂ < R_кр и R₁<R₂ < R_кр (табл. 4) зарисовать кривые при R₂ и R_3.

Таблица 4

Экспериментальные значения параметров процесса при R	αэ	Тэ	δэ	Qэ
Единица измерения
R2=
R3=

10. Установить R₄ > R_кр. Зарисовать кривую процесса колебаний.

11. Построить графики Т_э, α_Э, δ_Э, Q_Э= .

12. Сделать выводы по работе.

ОФОРМЛЕНИЕ ОТЧЕТА

Отчет должен включать:

- Название работы;

- Фамилии и инициалы исполнителей, № группы;

- Рисунок 1;

- Уравнение колебательного процесса в контуре и его решения для , , .

- Рисунок 2;

- Расчетные формулы;

- Выбранные значения L и C;

- Таблицу 1;

- Таблицу 2;

- Таблицу 3;

- Таблицу 4;

- Графики

= , =

= , = ;

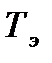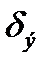- Рисунки осциллограмм колебаний при R₁, R_2, R₃, R₄;

- Выводы;

- Подписи исполнителей;

- Дату выполнения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назовите физический смысл коэффициента затухания.

2. Назовите физический смысл логарифмического декремента затухания.

3. Назовите физический смысл «добротности» контура.

4. Приведите аналогию электрических и механических колебаний.

5. Поясните влияние активного сопротивления R на процесс колебаний (от R= 0 до ).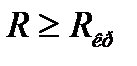

Литература

1. Савельев И.В. Курс общей физики. т.2. Электричество и магнетизм. Учебное пособие для втузов. М.:Наука,1978.

2. Лабораторные занятия по физике: Учебное пособие для вузов /Л.Л.Гольдин и др..; Под ред. Л.Л.Гольдина. М.: Наука, 1983.

3. Лабораторный практикум по физике: Учеб. Пособие для студентов вузов / В.Ф.Алексеев и др.; Под ред. К.А.Барсукова и Ю.И.Уханова. М.: Высшая школа, 1988.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н.ТУПОЛЕВА

Кафедра прикладной физики

Лабораторная работа

Дата добавления: 2015-08-02