Определение осевого массового момента инерции твердого тела методом физического маятника

Методические указания

Составители:

А.Х.Каримов

В.Т.Токарев

Казань 2000

УДК 53 (077)

Каримов А.Х., Токарев В.Т. Определение осевого массового момента инерции твердого тела методом физического маятника. /Методические указа­ния. Казань. Изд-во: Экоцентр. 2000 г. 9 с.

Приводится теория и методика определения осевого массового момента инерции твердого тела методом физического маятника. Результаты эксперимен­та обрабатываются методами прямых и косвенных измерений.

Табл. 1 Ил.2. Библиогр. –

Рецензент: доцент, к.ф-м.н. Е.И.Филатов

(Казанск. Гос.университет)

Цель заботы: изучить теорию колебаний физического маятника и методику определения осевого массового момента инерции твер­дого тела методом физического маятника.

Введение

При проектировании самолетов, ракет, космических и других летательных аппаратов, а также их двигателей необходимо знать осевые массовые моменты инерции отдельных деталей, узлов и всей конструкции.

Осевой момент инерции J твердого тела, вращающегося вокруг неподвижной оси, определяется по формуле

где m - масса тела; m_i - масса i -й материальной точки тела;

r_i - расстояние i -й точки от оси вращения.

Осевой массовый момент инерции тела характеризует распре­деление массы в теле и является мерой инертности тела при не­поступательном движении.

Массовый момент инерции тела входит в основное уравнение динамики вращательного движения твердого тела

где М - момент внешних сил; 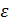- угловое ускорение тела,

Осевые массовые моменты инерции используются, например, для расчета:

-динамических характеристик летательных аппаратов (тра­ектории взлета, посадки, пикирования и т.д.);

-узлов и деталей летательных аппаратов на динамическую прочность. Например, стойки шасси самолета, механизма уборки и выпуска шасси, рулей высоты и направления, элеронов, крыль­ев и т.д.;

-собственных частот колебаний деталей и узлов;

-моделей летательных аппаратов при испытании их на штопор, флаттер и другие сложные аэродинамические явления;

-времени изменения режима вращения ротора газотурбинных двигателей.

Если деталь, узел крупногабаритные (крыло, корпус, фюзеляж), то осевые массовые моменты инерции определяются по частям (отсе­кам), а общий момент инерции находят как сумму моментов инер­ции этих частей. Во многих случаях моменты инерции определяют на геометрически подобных моделях.

Осевой массовый момент инерции определяют расчетным или экспериментальным путем.

В настоящее время для экспериментального определения осевых моментов инерции широко применяется метод физического маят­ника. При использовании этого метода исследуемая деталь или ее модель подвешивается при помощи двух призм (рис. К.2.1,а) или двух тонких гибких нитей одинаковой длины (рис. К.2.1.б).

Ось качаний должна быть горизонтальной и расположенной от центра тяжести (ц.т.) конструкции на расстоянии L.

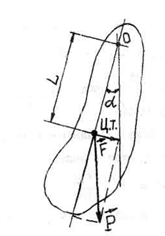
При малых отклонениях (до 6-10°) конструкция совершает при­близительно гармонические колебания, которые описываются соответствующим дифференциальным уравнением. Решение этого уравнения позволяет определить искомый момент инерции.

В данной лабораторной работе методом физического маятника определяют осевой массовый момент инерции произвольного тела.

Дата добавления: 2015-08-02