Теоретическая часть

Процессы зарядки и разрядки конденсатора изучаются на установке, электрическая схема которой показанана рис. 1.

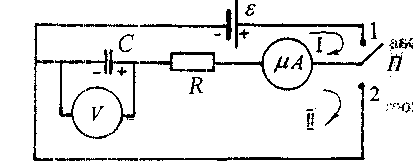
Рис. 1

Электрическая цепь представлена в виде контуров I и II. При замы­кании контура I переключателем конденсатор С заряжается через со­противление R до напряжения ε источника постоянной э.д.с.

При замыкании контура II конденсатор С разряжается через то же со­противление R. Микроамперметр и вольтметр позволяют регистрировать силу тока в контуре и напряжение конденсатора в различные моменты времени.

Рассмотрим процесс зарядки конденсатора. Применим к контуру I второе правило Кирхгофа «В замкнутом контуре разветвленной электрической цепи алгебраическая сумма падений напряжений I_iR_i на отдельных участках контура равна алгебраической сумме э.д.с 𝜀_I в контуре»:

IR+U=ε, (1)

где I - мгновенное значение силы тока заряда; R - сопротивление резисто­ра; U - мгновенное значение напряжения на конденсаторе.

Внутренним сопротивлением источника тока пренебрегли.

Направление обхода выбрали по часовой стрелке. Известно, что

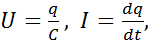(2)

где q - заряд конденсатора.

Используя равенства (2), преобразуем выражение (1) для определе­ния напряжения на конденсаторе к виду:

(3)

Уравнение (3) представляет собой дифференциальное уравнение первого порядка с постоянными коэффициентами. Для его решения введем переменную и = U-𝜀.. Тогда:

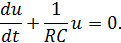
(4)

Решая уравнение (4), получим

u=u₀e^-t/RC,

где u₀ - постоянная интегрирования, зависящая от начальных условий. Если отсчет времени начать с момента замыкания контура I, то начальные условия примут вид:

t = 0, U =0, и = -𝜀, следовательно, u₀=𝜀.

Возвращаясь к первоначальной переменной U, получим выражение для напряжения на конденсаторе:

U=ε(1-e^-t/RC). (5)

При t = 0 из выражения (5) имеем U = 0. С увеличением времени tнапряжение на конденсаторе непрерывно увеличивается и асимптотически приближается к э.д.с. источника тока (рис. 2).

Подставив выражение (5) в уравнение: (1), получим зависимость за­рядного тока от времени:

Сила тока имеет наибольшее значение 1 = ε/R в начальный момент

времени t = 0 и асимптотически стремится к нулю в процессе заряд­ки (рис. 2).

Рис.2 Рис.3 Рис.4

При разрядке конденсатора, записывая второе правило Кирхгофа для контура II и учитывая выражение (2), получим уравнение для опреде­ления напряжения на конденсаторе:

Решение уравнения (7) записывают в виде:

U=U₀∙e^-t/RC.

Если время отсчитывать с начала процесса разрядки конденсатора, то начальными условиями будут:

t = 0, U₀=𝜀.

Окончательно зависимость напряжения на конденсаторе от времени разрядки примет вид:

U=𝜀∙e^-t/RC. (8)

При разрядке конденсатора, так же как и при зарядке, изменение силы тока в цепи определяется выражением (6).

Графики, показывающие характер изменения напряжения на конденса­торе и силы тока в цепи при разрядке конденсатора, приведены на рис. 3.

Как следует из графиков, напряжение и сила тока уменьшаются со време­нем по экспоненциальной зависимости, асимптотически приближаясь к нулю.

Из выражений (5), (6), (8) видно, что скорость изменения силы тока I в цепи и напряжения на конденсаторе U зависит от произведения

𝜏=RС,

называемого постоянной времени, или временем релаксации электриче­ского контура.

Подставляя R в омах, С в фарадах, получаем τ в секундах. Постоянная времени τ показывает, через какое время t = τ напряжение на конденсаторе или сила тока в цепи уменьшится в е = 2,71 раза.

Постоянную времени 𝜏 можно определить из формул (6) или (8). На­пример, преобразуя формулу (6)

получаем линейную зависимость 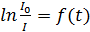(рис.4), для которой

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Ознакомиться с лабораторной установкой и измерительными прибо­рами.

2.Снять зависимости I=f(t), U=f(t) при зарядке и разрядке конден­сатора.

Значения I и U фиксировать, начиная с момента времени t= 0 че­рез каждые 5 секунд. Снять не менее 10 показаний и занести их в табл. 1. и табл. 2. Каждый опыт выполнить по 3 раза.

Таблица 1

Зарядка конденсатора

Регистрируемый Параметр		Время, с
I, мкА
Ср.
U, В
Ср.

Таблица 2

Раз р я дка конденсатора

Регистрируемый Параметр		Время, с
I, мкА
Ср.
U, В
Ср.

3. Рассчитать средние значения I и U и занести их в табл. 1 и 2.

4.Построить графики I=f(t), U=f(t) при зарядке и разрядке кон­денсатора.

5.Для одного значения времени записать полностью результат опреде­ления I или U и погрешности измерения по методике прямых изме­рений.

6.Определите постоянную времени τ_эксп. контура. Для этого заполнить

табл. 3 и построить график .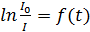
Таблица 3

Результат расчета		Время, с

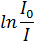
7. Рассчитать τ_расч по известным значениям емкости С и сопротивле­ния R лабораторной установки.

8. Вычислить относительную погрешность определения τ:

9. Для процесса разрядки конденсатора рассчитать начальное значение силы тока I_0расч по измеренному U₀ и известному сопротивлению цепи R. Сравнить I_0расч с I_0эксп и подсчитать относительную ошибку δ_I.

ОФОРМЛЕНИЕ ОТЧЕТА

Отчет по работе должен включать следующее:

1.Название и цель работы.

2.Краткую теоретическую часть.

3.Схему лабораторной установки.

4.Экспериментальную часть: табл.1, 2, 3; графики I=f(t), U=f(t) для зарядки и разрядки конденсатора; расчеты τ,δ_τ δ_I; I₀; расчет погрешности измерений.

5. Выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что такое конденсатор? Электрическая емкость, единица емкости?

2.Объясните порядок вывода зависимостей U=f(t),I=f(t) при за­рядке и разрядке конденсатора.

3.Назовите характеристику скорости зарядки и разрядки конденсатора, ее физический смысл и единицу.

ЛИТЕРАТУРА

1.Савельев И.В. Курс общей физики, т.2. Электричество и магнетизм. Учебное пособие для втузов. М.: Наука, 1978.

2.Лабораторные занятия по физике: Учебное пособие для вузов / Л.Л. Гольдин и др.; Под ред. Л.Л. Гольдина. М.: Наука, 1983

3.Лабораторный практикум по физике: Учеб. пособие для студентов втузов / В.Ф. Алексеев и др.; Под ред. К.А. Барсукова и Ю.И. Уханова. М.: Высшая школа, 1988.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им.А.Н.ТУПОЛЕВА

Кафедра прикладной физики

Лабораторная работа

Дата добавления: 2015-08-02