Теоретическая часть. Свободные колебания в системах происходят при отсутствии внеш­него воздействия за

Свободные колебания в системах происходят при отсутствии внеш­него воздействия за счет первоначально внесенной энергии. Свободные колебания механического маятника совершаются под действием силы тя­жести после начального отклонения его от положения равновесия.

В реальных колебательных системах вследствие рассеяния энергии свободные колебания всегда происходят с уменьшающейся по времени ам­плитудой, т.е. являются затухающими. В механических колебательных си­стемах причинами потерь энергии и затухания колебаний могут быть сопротивление среды, трение в точке подвеса и др.

Рассмотрим процесс колебаний маятника (рис.1) при малых отклонени­ях от положения равновесия и при на­личии силы сопротивления среды.

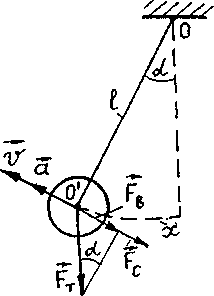
Рис.1. Схема колебаний маятника

О - точка подвеса маятника;

х - смещение маятника от положения равновесия

Считаем, что вся масса маятника длиной l и груза сосредоточена в точке О'. Следовательно, сила тя­жести маятника F _т = mg приложена в точке О'.

Пусть маятник с ускорением а движется влево. Уравнение движения материальной точки О' запишется в виде

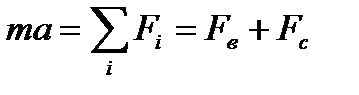, (1)

где F_в – сила, возвращающая маятник в положение равновесия, F_c – сила со­противления среды движению маятника.

Возвращающая сила, определяемая силой тяжести F _т,

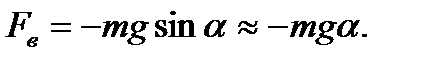(2)

Знак минус показывает, что вектор силы F_в направлен против век­тора ускорения а. При малых углах отклонения sin α ≈ α.

Сила сопротивления среды F _c также действует против направле­ния ускорения а маятника и при небольших скоростях пропорциональ­на скорости V движения

F _с = 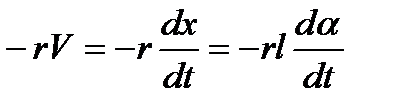, (3)

где r - коэффициент сопротивления среды, х - смещение маятника от положения равновесия (рис.1).

Выразим линейное ускорение а в уравнении движения (1) через уг­ловое ускорение ε

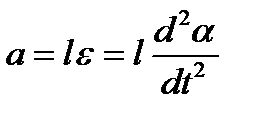, (4)

Подставляя выражения (2), (3), (4) в (1), получим

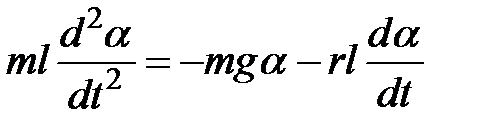
и после преобразований -

.

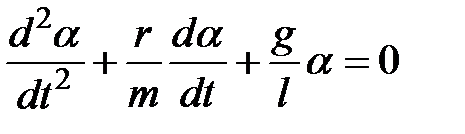Обозначим , .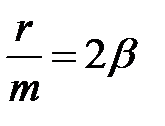

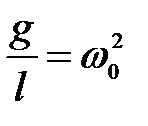Уравнение свободных затухающих колебаний окончательно записывается в виде

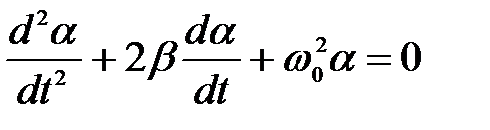, (5)

Известно, что свободные незатухающие колебания математического маятника без потерь описываются дифференциальным уравнением .

Величина ω ₀ называется циклической частотой собственных незатухающих колебании системы. Зная период Т ₀ и частоту 𝜈 ₀ незатухающих колебаний, циклическую частоту незатухающих колебаний определяют как .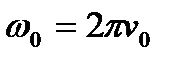

Таким образом, в уравнении (5) ω ₀ также является циклической частотой собственных незатухающих колебаний системы без потерь.

В зависимости от соотношения коэффициентов 2β и диффе­ренциальное уравнение (5) имеет несколько решений.

Рассмотрим решение этого уравнения при условии 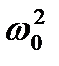>> 2β. В этом случае решение уравнения записывается в виде

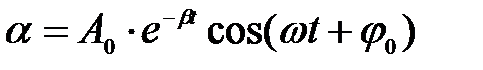, (6)

где А₀ и φ₀ - соответственно начальная амплитуда и начальная фаза колебаний, определяемые из начальных условий.

Величина

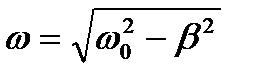(7)

называется циклической частотой затухающих колебаний.

Так как затухание нарушает периодичность колебаний, то зату­хающие колебания не являются строго периодическими. При малых по­терях, а, следовательно, и малом затухании затухающие колебания толь­ко приблизительно считаются периодическими. Условный период Т колебаний определяется как промежуток времени между двумя соседними максимумами или минимумами амплитуды.

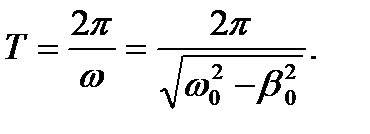(8)

График функции (6) приведен на рис 2. Амплитуда затухающих колебаний уменьшается по экспоненци­альному закону

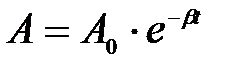. (9)

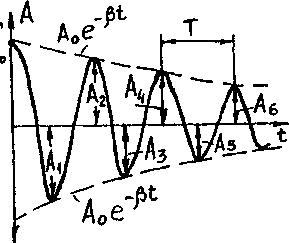
Рис.2. График затухающих колебаний

Чем больше коэффициент β, тем быстрее затухает амплитуда колеба­ний. Поэтому величину β назы­вают коэффициентом затухания.

Более ясный физический смысл имеет величин, обратная коэффи­циенту затухания

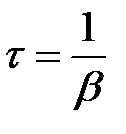(10)

и называемая постоянной времени (время релаксации) колебательной си­стемы. Если подставить выражение (10) для τ в формулу (9) измене­ния амплитуды, то при t = τ получим

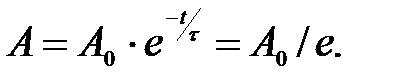
То есть постоянная времени τ – это время, за которое амплитуда колебаний уменьшается в е раз (е ≈ 2,718).

Для количественной характеристики скорости уменьшения ампли­туды вводится характеристика, называемая логарифмическим декремен­том затухания δ и равная натуральному логарифму отношения ампли­туд в моменты времени t и (t + T)

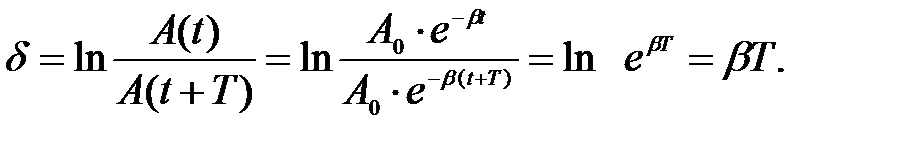(11)

Более явный физический смысл имеет величина, обратная логарифмическому декременту затухания

,

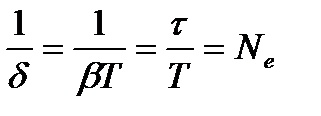N_e - число колебаний, за которое амплитуда А уменьшится в е раз.

Для характеристики качества колебательной системы вводится по­нятие добротности Q. Добротностью называют отношение энергии E(t) колебательной системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t + T, т.е. за один период затухающих колебаний

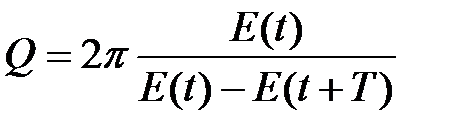(12)

Так как энергия E (t) пропорциональна квадрату амплитуды колебаний A(t), то

.

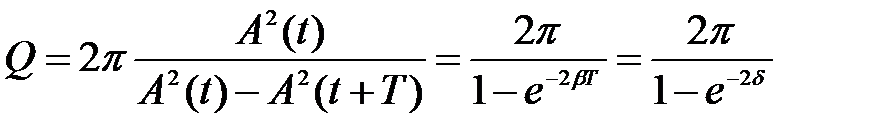При δ << 1 1 – e ^-2δ ≈ 2 δ, ω ≈ ω₀, T ≈ T₀

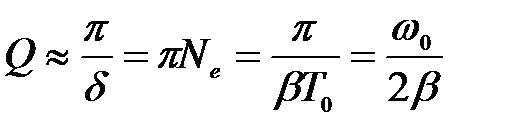(13)

Например, камертон имеет δ ≈10^-3, N_e =10³ и Q = 3, 14 · 10³.

Практическая часть работы

Описание лабораторной установки

Лабораторная установка для изучения затухающих колебаний ма­ятника состоит из маятника и шкалы для отсчета амплитуд колебаний в угловых градусах.

Маятник представляет собой штангу, на нижнем конце которой установлен диск - груз со стрелкой. Верхний конец штанги закреплен в цилиндрическом шарнире неподвижной стойки.

Выполнение работы

1. Определение периода колебаний маятника.

- Отклонить маятник на 5°, отпустить и замерить время t 5-ти полных колебаний маятника. Опыт повторить еще 2 раза.

- Записать результат трех опытов определения времени t пяти пол­ных колебаний маятника по методике обработки результатов прямых из­мерений.

- Период Т колебаний маятника определить по среднему арифметическому значению t_ср.

2. Определение амплитуд колебаний маятника.

- Отклонить маятник A₀ = 5°, например, вправо. Отпустить. Из­мерить четные амплитуды колебаний (рис. 2) А₂, А₄, А₆, А₈, А₁₀. Опыт повторить еще 2 раза.

Результаты занести в табл. 1

A₀ = 5° Таблица 1

№ опыта	Амплитуда, град
А2	А4	А6	A8	А10	А1	А3	А5	A7	А9
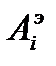
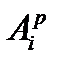
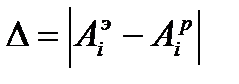
εmax

- Провести аналогичные измерения нечетных амплитуд А₁, А₃, А₅, А₇, А₉.

-Рассчитать средние экспериментальные значения амплитуд .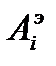

- По экспериментальным значениям Т, A₀, 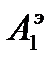, , 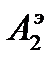… построить график затухающих колебаний, аналогичный рис.2.

3. Расчет параметров затухающих колебаний маятника.

- Рассчитать три значения δ₁, δ₂, δ₃ логарифмического декремента
затухания, принимая соответственно соотношения соседних амплитуд
A₀ / А₂, А₂ / А₄, А₄ / А₆. Вычислить среднее арифметическое значение δ.

- Рассчитать коэффициенты затухания β, время релаксации τ и добротность Q маятника.

- Рассчитанные значения Т, δ, β, τ, Q занести в табл. 2.

Таблица 2

Т, с	δ	β, с^-1	τ, с	Q

4. Построение расчетного графика затухающих колебаний.

- Зная A₀, β, полагая начальную фазу ω₀ = 0 и вычислив ω = 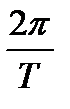, записать уравнение затухающих колебаний маятника.

- По полученному уравнению колебаний рассчитать амплитуды 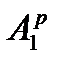, , 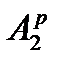, , 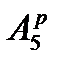и т.д. (табл.1).

- На рисунке с экспериментальной кривой построить расчетный
график затухающих колебаний.

- Определить абсолютные разницы ∆ экспериментальных и рас­четных значений амплитуд колебаний и наибольшую относительную разницу 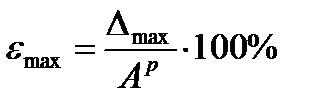(табл. 1).

5. Сделать выводы по работе.

Контрольныевопросы

1. Какой колебательный процесс называется затухающим?

2. Запишите уравнение затухающих колебаний.

3. Дайте определение параметров затухающих колебаний: коэффициента затухания, логарифмического декремента затухания, времени ре­лаксации, добротности.

4. Как изменятся график и параметры колебаний при увеличении за­тухания?

Список литературы

1. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989. 607с.

2. Савельев И.В. Курс общей физики. В 3-х т. T.I. M.: Наука. 1989.
352с.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н.ТУПОЛЕВА

Кафедра прикладной физики

Лабораторная работа

Дата добавления: 2015-08-02