Краткая теория физического маятника

Физическим маятником называется твердое тело, совершающее под действием силы тяжести (рис. К.2.2) колебания вокруг гори­зонтальной оси (подвеса).

После отклонения тела на угол αоно возвращаетсяв положение равновесия под действием силы 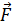, являющейся тангенци­альной составляющей силы тяжести .

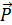Момент силы 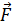относительно оси 0 равен

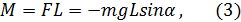
Здесь знак силы 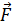противоположен знаку угла поворота маятника и знаку sinα.

Основное уравнение (2) динамики вращательного движения твердого тела записывается в виде

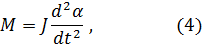
Подставляя выражение для момента внешней силы (3) в выра­жение (4), получим

Уравнение (5) является дифференциальным уравнением качаний физического маятника.

При малых углах отклонения маятника sin α ≈ α и уравнение (5) принимает вид:

Уравнение (6) представляет собой дифференциальное уравне­ние гармонических колебаний, записываемое обычно в виде

где 𝜔 ₀ - циклическая частота колебаний, равная

, Т - частота и период колебаний.

Решение уравнения (6) имеет вид

α=α₀cos(ωt+φ₀), (9)

где α₀, - амплитуда колебания угла α, φ₀ - начальная фаза колебаний.

Изуравнений (6), (7) и (8)определяется период колебаний физического маятника

Осевой массовый момент инерции тела, качающегося вокруг

точки подвеса С, определяется из формулы (10)

Порядок выполнения работы

1. Ознакомиться с лабораторной установкой и моделью, момент инерции которой необходимо определить.

2. Измерить на исследуемой модели расстояние L от оси подвеса до цента тяжести.

3. Определить период Т качаний модели, отклоняя ее на 10-15° и замеряя время 10 полных качаний модели.

4. Повторить пункт 3 еще четыре раза.

5. Записать исходные данные и результаты опыта в таблицу

№ опыта	Время 10-ти качаний t, c	T, c

Т_ср= … с.

6. Обработать результаты измерения периода колебаний по методу прямых измерений. Оценить погрешности и записать результаты измерений.

7. Вычислить осевой массовый момент инерции модели. Массамодели крыла равна 0,74 кг, стабилизатора - 0,54 кг.

8. Определить относительную, абсолютную погрешности момента
инерции методом косвенных измерений.

При расчетах учитывать ∆T, ∆L=0,001 м и ∆m=10^-3 кг.

9. Записать результат косвенного измерения момента инерции в виде

J=J±∆J, n=, p=.

10. Отчет по лабораторной работе должен включать следующее:

- наименование работы;

- цель работы;

- расчетные формулы с пояснением входящих в них величин;

- эскиз экспериментальной установки с обозначением основ­ных деталей и параметров, входящих в расчетную формулу;

- таблицу с экспериментальными данными;

- расчет определяемого параметра и его погрешностей;

- анализ полученных результатов.

Контрольные вопросы

1. Что называется физическим маятником? В чем его отличие от математического маятника?

2. Чем отличается уравнение колебаний физического маятника от уравнения колебаний математического маятника?

3.Что характеризует осевой массовый момент инерции твер­дого тела? В чем заключается его влияние на движение тела?

4. Расскажите последовательность определения момента инер­ции твердого тела методом физического маятника.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н. Туполева

Кафедра прикладной физики

А.Х. Каримов, Р.Х. Макаева, В.Т. Токарев

Дата добавления: 2015-08-02