|
Читайте также: |
Примерами применения законов сохранения импульса и энергии являются соударения тел.
Соударением, или ударом, называют столкновение тел, при котором взаимодействие тел длится малое время (10-4...10-5 с), а развивающиеся на площадках контакта ударные или мгновенные силы велики (Р до 104...105 кгс/см2). Это позволяет пренебречь действующими на сталкивающиеся тела внешними силами и систему тел рассматривать как замкнутую механическую систему, к которой применимы законы сохранения.
Следствиями удара могут быть остаточные деформации, нагревание тел, изменение механических свойств материалов тел, а при скоростях удара больше критических - разрушение тел. Например, критические скорости составляют для стали 150 м/с, меди 15 м/с.
Процесс соударения двух тел разделяют на две фазы. Первая фаза начинается с момента соприкосновения точек А и В тел (рис. 1). Прямая п, проходящая через точки соприкосновения точек А, В, и нормальная к поверхности тел называется линией удара. Пусть скорость движения первого тела v1, второго – v2, а точки C1 и C2- центры тяжести тел.
Проекциями скоростей v A и v B на линию удара (общую нормаль) являются vAn и v Bn. Следовательно, относительная скорость сближения точек А и В тел до удара будет равна vAn - vBn. К концу 1-й фазы удара сближение тел прекращается. Часть их кинетической энергии переходит в потенциальную энергию деформации.
Во второй фазе потенциальная энергия упругой деформации обратно переходит к кинетическую энергию тел. Тела начинают расходиться и
к концу 2-ой фазы точки А и В будут иметь относительную скорость расхождения v'An – v’ Bn. Для абсолютно упругих тел механическая энергия
восстанавливается полностью и | vAn — vBn | = | v'An — v’Вп |. Удар абсолютно неупругих тел заканчивается на первой фазе и v'An — v’Вп= 0.
При ударе реальных тел механическая энергия к концу удара восстанавливается лишь частично из-за потерь на остаточные деформации и нагревание тел. Поэтому | v'An — v’Вп | < | vAn — vBn |. Для учета этих потерь вводится коэффициент восстановления К, равный отношению нормальных составляющих относительной скорости тел до и после удара.
Коэффициент восстановления К определяется экспериментально и зависит от физических свойств материалов тел. Например, при соударении тел из дерева К ≈ 0,5, из стали - 0,55, из стекла - 0.94, из свинца - 0. Для абсолютно упругого удара К = 1, а абсолютно неупругого К = 0.
Если центры тяжести тел C1и С2 лежат на линии удара, то удар называется центральным. Удар считается прямым при скоростях движения тел v1, и v2, параллельных линии удара. В обратных случаях удар является нецентральным и косым.
Наиболее полно разработана теория удара абсолютно упругих тел. Задача удара неупругих тел является более сложной.
Рассмотрим краткую теорию центральных прямых абсолютно упругих и абсолютно неупругих ударов.
Абсолютно упругим ударом называют соударение двух тел, при котором суммарные кинетические энергии соударяющихся тел до и после удара равны. При этом сначала кинетическая энергия тел полностью переходит в потенциальную энергию упругой деформации тел и далее происходит обратный переход. Остаточные деформации тел отсутствуют.
Для абсолютно упругого удара выполняются законы сохранения суммарного импульса и полной энергии.
Пусть v1, и v2 - скорости шаров массами m1 и т2 до удара, а v’1, и v’2- после удара (рис.2).
Рис.2
Рис.2 Уравнения сохранения импульса и энергии запишутся в виде
m1v1 + m2v2 = m1v’1 + m2v’2
(2)
В результате решения этой системы уравнений получают
(3)
(4)
Рассмотрим некоторые частные случаи абсолютно упругого удара.
Пусть скорость второго тела до удара равна нулю, т.е. v2 = 0.
а) Если т1= т2, то из уравнений (3) и (4) следует, что v’1 = 0, а
v’2 =v1; т.е. послеудара первый шар остановится, а второй - будет двигаться в
том же направлении со скоростью первого шара v’2 =v1.
б) При т1> т2 оба шара будут двигаться в том же направлении: первый
с v’1 =v1, второй - с v’1 < v’2 < v1.
в) Если т1< т2, то первый шар отскакивает в обратную сторону, а
второй шар будет двигаться в направлении первого до удара с v’1< v1.
При т2=т1 из формул (3) и (4) получаем v’1 = v2 и v'2 = v1, т.е. при соударении шаров равной массы они «обмениваются» скоростями.
Близкими к абсолютно упругим ударам считают столкновение двух упругих твердых шаров, например, бильярдных; столкновения между атомами, ядрами, элементарными частицами.
Абсолютно неупругим ударом называют столкновение двух тел, при котором тела «слипаются» и движутся далее как одно целое. При таких соударениях часть начальной кинетической энергии превращается в тепловую и затрачивается на остаточную деформацию тел. Поэтому суммарная кинетическая энергия механической системы не сохраняется, а уменьшается. Суммарный импульс тел остается постоянным.
В этом случае закон сохранения импульса системы в общем виде (без учета знаков) записывают в виде:
m1v1 + m2v2 = (m1+ m2)v’
где v’ = v’1 = v’1- скорость «слипшихся» после удара тел. Отсюда
(5)
Если массы тел равны m1 = m2, то
Примерами абсолютно неупругого удара являются столкновение шаров из пластилина, глины, сцепление двух железнодорожных вагонов при движении.
Если в формуле (5) принять v2 = 0 и т2>> т1, то получается v’<<v1, т.е. почти вся кинетическая энергия переходит в другие формы энергии.
Примерами неупругих ударов служат ковка, штамповка, клепка, забивание свай, гвоздей, перемещение в среде с большим сопротивлением.
СОДЕРЖАНИЕ РАБОТЫ
Рассматривается центральный удар двух шаров 1 и 2 массами m1 и m2, подвешенных на нитях длиной l1 =l2 =l (рис. 3).
Шар 1, отклоненный на первоначальный угол α1 перед соударением развивает скорость v1. Её можно определить из закона сохранения энергии: 
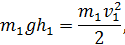
Где h1 - высота подъема центра шара 1, соответствующая начальному углу α1. Так как
, то
(6)
После соударения шар 2 приобретает скорость v’2 определяемую аналогично:
(7)
При выводе формул (6) и (7) пренебрегли потерями энергии на сопротивление воздуха и трение в подвесах.
Задание 1
1.Подвесить два одинаковых стальных шара диаметрами d= 20 мм. Следовательно, m1=m2=m
2. Шар 2 установить в равновесное положение α2= 0, v2= 0, а шар 1 отвести на начальный угол α1= 10°.
3. Отпустить шар 1 и после соударения по шкале измерить угол α’2 отклонения шара 2. Результат записать в таблицу 1.
4. Согласно теоретической части при m1=m2, v2=0 и абсолютно упругом ударе шар 1 после соударения должен остановиться (v’1 = 0).
Убедитесь в этом на опыте.
5.Повторить п.п. 2 и 3 еще 4 раза.
Таблица 1
| № измерения | α'2ср,0 | |||||
| α'2,0 |
6.Обработать результаты пяти измерений угла α'2 по методике прямых измерений. Записать результат прямых измерений.
7.Вычислить объем и массу шаров.
8.По формуле (6) определить скорость v1 шара 1 перед соударением и импульс p1=mv1.
9.По формуле (7) рассчитать скорость v’2 шара 2 после соударения, которая обеспечит подъем шара 2 на высоту h’2 и отклонение на угол α'2. Определить импульс шара 2 р’2= mv’2.
10.Вычислить коэффициент восстановления скорости
11. Сделать вывод о соответствии выполненного опыта случаю абсолютно упругого удара.
Задание 2
1. В качестве шара 1 подвесить стальной шар диаметром d = 36 мм, а в
качестве шара 2-стальной шар диаметром d= 20мм.
Следовательно, т1 >m 2.
2. Шар 2 установить в равновесное положение α2= 0, v2 = 0, а шар 1 отвести на начальный угол α1 = 10°.
3.Отпустить шар 1 и после соударения по шкале измерить угол α'2 отклонения шара 2. Результат записать в табл. 2.
4.Согласно теоретической части при т1>т2,v2= 0 и абсолютно
упругом ударе шары 1 и 2 после соударения будут двигаться в одном
направлении со скоростями v1, v2 и отклонятся на углы α'1 и α'2.
5. Повторить пункты 2 и 3 еще 4 раза.
6.Повторить пункты 2 и 3 пять раз для измерения угла α'1 отклонения шара 1 после соударения.
Таблица 2
| № измерения | α'ср,0 | |||||
| α'2,0 | ||||||
| α'1,0 |
7.Обработать результаты измерений углов α'2 и α'1 по методике прямых измерений. Записать результат прямых измерений.
8.Вычислить объемы и массы шаров.
9.По формуле (6) определить скорость v1 шара 1 перед соударением и импульс p1=mv1.
10. По формуле (7) рассчитать скорости v’1 и v’2 шаров после соударения. Определить импульсы р’1 и р’2 и суммарный импульс р’= р’1 + р’2
11.Вычислить коэффициент восстановления скорости
12. Определить, на сколько уменьшился передаваемый импульс.
13.Сделать вывод о соответствии выполненного опыта случаю
абсолютно упругого удара.
Задание 3
1. В качестве шара 1 подвесить стальной шар диаметром d = 20 мм, а в качестве шара 2 - пластилиновый.
2. Пластилиновый шар 2 установить в равновесное положение α2 =0, v2=0, а стальной шар 1 отвести на начальный угол α1 = 10°.
3. Отпустить шар 1 и после соударения по шкале измерить угол α'2 отклонения пластилинового шара 2. Результат записать в табл. 3.
4.Согласно теории абсолютно неупругого удара после соударения шары «слипаются» и двигаются в с одной скоростью v’= v’1 = v'2. Убедитесь в этом на опыте.
5. Повторить пункты 2 и 3 еще 4 раза
6. Обработать результаты пяти измерений угла α'2 по методике прямых измерений. Записать результат прямых измерений.
Таблица 3
| № измерения | -1 | α'2ср,o | ||||
| α'2,o |
7. Вычислить объемы и массы шаров.
8. По формуле (6) определить скорость v1 шара 1 перед соударением и импульс p1=mv1.
9. По формуле (7) рассчитать экспериментальные значения скорости v’2= v’1= v’э шара 2 после соударения.
10. По формуле (5) рассчитать теоретическое значение скорости v'paсч шаров после соударения.
11. Определить расхождение v’э и v'paсч:
12.Вычислить суммарный импульс шаров после соударения
р' = v’э(m1+ т2).
13.Сравнить значения импульсов р1 и р' с истемы до и после
соударения.
14. Сделать вывод о сохранении импульса и о виде соударения.
Контрольные вопросы
1. Две фазы процесса соударения тел.
2. Коэффициент восстановления кс-
3. Абсолютно упругий удар и его частные случаи.
4. Абсолютно неупругий удар.
Казанский государственный технический университет
им. А.Н. Туполева
Кафедра прикладной физики и химии
А.Х. Каримов, Е.Л. Каспин
Лабораторные работы по физике
Дата добавления: 2015-08-02; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ТЕОРЕТИЧЕСКАЯ ЧАСТЬ | | | Стрелочные электроизмерительные приборы. |