Теоретическая часть. Вращательное движение твердого тела относительно неподвижной оси OZ

Вращательное движение твердого тела относительно неподвижной оси OZ, проходящей через центр масс (рис. 1), под действием внешнего момента М силы F описывается уравнением динамики вращательного движения твердого тела:

M =J ∙ɛ (1)

где М = [ г∙F ] - момент силы;

J - осевой массовый момент инерции твердого тела относительно неподвижной оси OZ, проходящей через центр масс;

ɛ - угловое ускорение;

г - радиус - вектор точки А приложения силы F.

Модуль момента силы равен М = F ∙ r ∙ sinα= F ∙ l,

  Рис. 1

где l - плечо силы F относительно оси

OZ, перпендикулярное направлению силы F.

Осевым массовым моментом инерции твердого тела (далее момент инерции ) относительно неподвижной оси вращения называется физическая величина, равная сумме произведений масс т_i n материальных точек твердого тела на квадрат их расстояний r_i до рассматриваемой оси

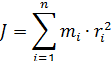
(2)

Единица измерения момента инерции в СИ – кг∙м².

Момент инерции характеризует распределение массы тела по радиусу относительно оси вращения и является мерой инерции тела при его вращательном движении.

Два тела, вращающиеся под действием одинаковых внешних моментов М и имеющие разные моменты инерции J, будут раскручиваться с разными ускорениями. Тело, имеющее меньший J, раскручивается быстрее.

Авиационный газотурбинный двигатель, с меньшим моментом инерции ротора, быстрее наберет требуемые обороты, а самолет с этим двигателем сделает соответственно более быстрый маневр (набор высоты, вираж и т.д.).

Уравнение (1) по физическому смыслу аналогично второму закону Ньютона

F = т∙ а, (3)

В левых частях уравнений (1) и (3) стоят физические величины М и F - причины движения, в правых частях - меры инертности тела J и т и ускорения ɛ и а.

Момент инерции вращающегося тела простой геометрической формы (сплошной диск, шар, цилиндр и др.) можно рассчитать аналитически.

Для тела сложной геометрической формы и при неравномерном распределении массы вращающегося тела по радиусу относительно оси массовый момент инерции определяется экспериментальным способом.

Рассмотрим это на примере диска 1 сложной геометрической формы (рис.2), вращающегося вокруг оси, проходящей через центр масс.

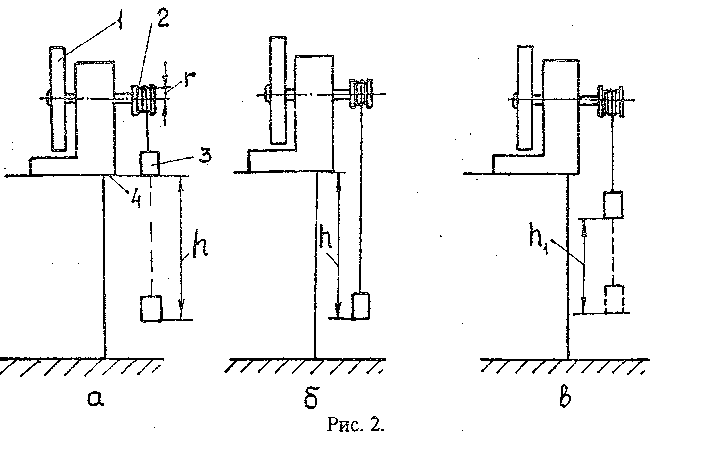
К шкиву 2 прикреплена нить длиной l с грузом 3 массой т.

Вращая диск, наматывают нить на шкив и груз поднимают на высоту h от нижнего положения. Поднятый груз приобретает потенциальную энергию mgh (рис. 2, а).

Если груз отпустить, то он под действием силы тяжести будет падать вниз, натягивая нить и вращая диск. Падение груза продолжается до нижнего положения, определяемого длиной нити. Высота падения груза равна h (рис. 2, б). При падении потенциальная энергия груза преобразуется в кинетическую энергию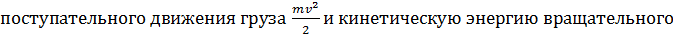

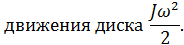
Часть потенциальной энергии затрачивается на работу по преодолению сил трения в опорах

А = F_mp h.

Согласно закону сохранения энергии

где т - масса груза;

h - высота падения груза;

v- скорость поступательного движения груза;

J - момент инерции диска;

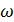- угловая скорость вращения диска;

F_mp - сила трения.

Для расчета момента инерции J диска физические величины v, и F_mp можно выразить через экспериментально измеряемые высоту h и время t падения груза.

Так как движение груза равноускоренное, то его скорость равна:

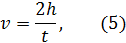
где t - время падения груза.

Угловая скорость вращения диска

где г - радиус шкива 2 (рис. 2, а).

Сила трения F_mp рассчитывается следующим образом. Груз массой т, падая с высоты h, достигает низшей точки, ограничиваемой длиной нити. Раскрученный диск продолжает вращаться по инерции, наматывая нить на шкив. Вследствие этого груз поднимается на высоту h₁ < h (рис.2, в). Приобретенная при таком подъеме груза потенциальная энергия выразится как mgh ₁.

Убыль потенциальной энергии обусловлена расходом ее на преодоление сил трения

mgh – mgh₁ = F_mp (h+ h₁).

Отсюда

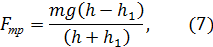
Окончательная формула для расчета момента инерции получается при подстановке выражений (5), (6), (7) в формулу (4)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Определить радиус г шкива 2 (рис. 2. а), измерив штангенциркулем его диаметр. Измерение произвести один раз, результат занести в таблицу.

Значение массы груза, указанного на нем, так же занести в таблицу.

r=; m=; h=; Таблица

Номер опыта	h1, м	t, с

h_1ср=; t_ср=;

2. Прикрепить нить одним концом к шкиву, другим - к грузу. Вращая диск, установить груз нижним торцом по нижней плоскости основания установки 4 (рис. 2, а).

3. Отпустить шкив. Измерить линейкой с точностью до 1 мм высоту h падения груза. Измерение провести один раз и результат занести в таблицу.

4. Повторно поднять груз, и определить с точностью до 0,01 с время t падения груза с высоты h. Результат занести в таблицу.

Повторить измерение времени t падения груза еще 2 раза.

5.Определить высоту h₁ подъема груза диском при его вращении по
инерции. Измеренное значение нести в таблицу.

Повторить измерение h₁ еще 2 раза.

6.Обработать результаты измерения времени t падения груза с высоты h и высоты h₁ подъема груза по методике обработки результатов прямого измерения.

7.Определить момент инерции J диска по методике косвенных измерений. При расчетах принимать переменными величинами т, h₁, t, а ∆m= 10^-3 кг.

6. Отчет по лабораторной работе должен включать:

- краткую теоретическую часть;

- схему установки (рис. 2);

- таблицу;

- расчеты и запись результатов прямых измерений h₁, t;

- расчеты и запись результата косвенного измерения J;

- выводы по работе.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется моментом инерции? Единицы его измерения?

2.Что является мерой инертности тела при поступательном и вращательном движениях?

3.Как будет двигаться диск при отсутствии трения?

4.Выведите расчетную формулу для момента инерции.

СПИСОК ЛИТЕРАТУРЫ

1. Детлаф А.А.. Яворский Б.М. Курс физики. М.: Высшая школа, 1989.607 с.

2. Савельев И.В. Курс общей физики. В 3 s т. Т. 1.. М.: Наука. 1989.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н. Туполева

Кафедра технической физики

Дата добавления: 2015-08-02