Вынужденные электромагнитные колебания

Составитель А.Х.Каримов

Казань - 2000

УДК 53

Каримов А.Х. Вынужденные электромагнитные колебания. / Лабораторная работа. Казань; Изд-во «Экоцентр». 2000. 9 с.

Рассматривается краткая теория вынужденных колебаний в электрическом колебательном контуре. Приводится описание лабораторной установки и после­довательность проведения эксперимента.

Табл. -1. Ил. - 4. Библиограф: 3 назв.

Рецензент: к.ф-м.н., доцент КГУ Е.И.Филатов

Цель работы: Изучить процесс вынужденных электромагнитных колеба­ний. Построить резонансную кривую электрического колебательного контура, оп­ределить ее параметры, оценить влияние активного сопротивления контура.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В цепи электрического колебательного контура (рис.1) включен генератор гармонических колебаний, ЭДС которого изменяется по закону

ε(t)=𝜀₀sin Ω t (1)

где 𝜀₀ - амплитуда, Ω - частота колебаний ЭДС внешнего источника.

Рис.1.

В каждый момент времени согласно правилу Кирхгофа сумма ЭДС самоин­дукции 𝜀_L, падений напряжение на конденсаторе U_C и резисторе U_R равна внешней ЭДС генератора

𝜀_L+U_C+U_R=(t) (2)

После преобразований уравнения (2) с учетом того, что

дифференциальное уравнение изменения силы тока в контуре записывают

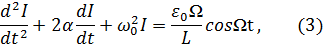
где 𝜔₀ - собственная частота колебаний контура при R =0,

α- коэффициент затухания колебаний.

Уравнение (3) является неоднородным линейным дифференциальным урав­нением 2-го порядка. Его общее решение складывается из общего решения одно­родного дифференциального уравнения и частного решения неоднородного урав­нения (3).

Первое решение представляет собой собственные затухающие колебания контура. Его можно не учитывать, так как собственные колебания контура, воз­никшие в начальный момент времени, быстро затухают. Частное решение урав­нения (3) записывают в виде

I=I₀sin(Ωt-φ), (4)

где

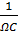- емкостное сопротивление, ΩL - индуктивное сопротивление и z - полное сопротивление колебательного контура, фаза колебаний

Вынужденные колебания в электрическом контуре устанавливаются через не­которое время (рис.2), так как возникающие в начальный момент собственные зату­хающие колебания контура препятствуют внешней ЭДС. Время установления выну­жденных колебаний контура равно времени затухания собственных колебании.

Зависимость (5) графически представляется кривой, приведенной на рис.3. При Ω=0- имеем постоянный ток, который конденсатор не пропускает. Следо­вательно, при Ω= 0 I₀ = 0.

Рис.2.

С увеличением частоты Ωвнешней ЭДС увеличивается амплитуда силы тока Iо в контуре и при

I₀ достигает: своего максимального значения

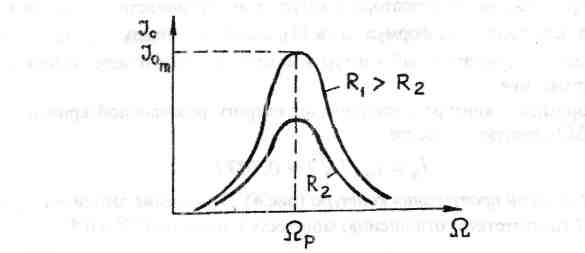
Рис.3.

При дальнейшем увеличении Ω амплитуда силы тока I₀ асимптотически приближается к нулю.

С увеличением активного сопротивления R кривая опускается ниже.

Из выражений (5) и (7) следует, что максимальная амплитуда тока будет наблюдаться при

Явление резкого увеличения амплитуды колебаний системы при совпаде­нии частоты воздействия внешнего источника ЭДС с собственной частотой коле­бательной системы называется резонансом.

Кривая зависимости I₀=f(Ω) (рис.3) называется резонансной кривой.

Частота собственных колебаний реального контура

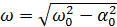, (10)

Резонанс наступает при Ω_р =ω_о>ω. Однако, при малом затухании контура (малые потери) ω_о≈ω.

Амплитуда напряжения на конденсаторе в момент резонанса

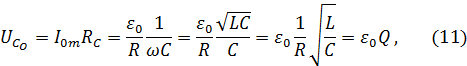
где Q - добротность контура.

Аналогично амплитуда напряжения на индуктивности

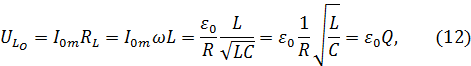
Таким образом, при резонансе напряжения на конденсаторе и катушке ин­дуктивности имеют одинаковые амплитуды.

Фазовый анализ колебательного процесса показывает, что в момент резо­нанса напряжение на конденсаторе и катушке индуктивности находятся в противофазе. И, как следует из формул (6) и (7), сдвиг фаз между ε_o и I φ= 0. Следовательно, колебательный контур в момент резонанса ведет себя как актив­ное сопротивление.

Добротность контура характеризует остроту резонансной кривой. Ширину кривой ∆Ω, взятую на высоте

называют полосой пропускания контура (рис.4). Отношение амплитуд I₀ и I_0m, равное 0,7 соответствует отношению мощностей, равному 0,7² ≈ 0,5.

Рис.4.

Относительной шириной полосы пропускания контура называют отношение

равное обратной величине добротности. Чем больше добротность контура, тем уже относительная ширина полосы пропускания контура и тем сильнее выделяет­ся резонансная частота.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Описание установки

Лабораторная установка состоит из лабораторного устройства, содержаще­го колебательный контур (рис.1) и систем его питания, а также подключенного к нему осциллографа.

Установка работает в 2-х режимах: затухающих и вынужденных колебаний.

В режиме вынужденных колебаний электрический колебательный контур питается от генератора, имеющегося в устройстве. На экран осциллографа выве­дены колебания напряжения на резисторе контура

U_R=IR.

На передней панели устройства вынесены следующие органы управления:

- «Сеть» - тумблер включения сети;

- «Режим» - тумблер режима работы устройства;

- «Затух» - затухающие колебания;

- «Вынужд» - вынужденные колебания;

- Тумблер переключения емкости контура С= 0,05 и 0,1 мкФ;

- Тумблер переключения индуктивности контура L= 0,5 и 1,0 Гн;

- Ручка R - изменения активного сопротивления в цепи контура;

- Ручка управления частотой f внутреннего генератора при работе в режиме вы­нужденных колебаний (от 0,19 до 4,5 кГц);

№ деления шкалы
f, кГц	0,19	0,21	0,24	0,28	0,34	0,42	0,52	0,79	1,4	4,5

-Гнездо «Осцил» - подключении осциллографа.

Подготовка к работе

1.Ознакомиться с теоретической частью и лабораторным устройством.

2.Установить тумблер режима в положение «Вынужд».

3.Ручку R поставить на наименьшее значение сопротивления.

4.Тумблеры С и L поставить в произвольные положения.

5.Включить лабораторное устройство и осциллограф в сеть.

6.Включить лабораторное устройство и осциллограф тумблерами «Сеть» и «Питание». Прогреть их в течение 2-3-х минут.

7.Получить устойчивую картину колебаний, регулируя ручками осциллографа (например, для осциллографа С1-73 ручками «Развертка», «Стаб», «Уровень»,

Выполнение работы

1. При заданных значениях R₁, L, C снять резонансную кривую колебательно­го контура U_R=f(t). В первом приближении частоту генератора можно определять по его шкале. Более точно частота генератора определяется путем измерения периода коле­баний Т с помощью осциллографа. Для построения резонансной кривой необходимо иметь 8-10 точек (табл.1).

L= Гн, C= мкФ, R₁= кОм Табл.1

Период Т,с
Частота f,Гц
UR	в делениях
В

2. По данным таблицы 1 построить график резонансной кривой колебательного контура.

3. Установить сопротивление резистора контура R₂>R₁.

Снять резонансную характеристику контура при R₂.

Данные измерений занести в табл.2, аналогичную табл. 1.

4. Построить резонансную кривую при R₂

5. По снятым резонансным кривым определить добротности контура при R₁ и R₂.

6. Рассчитать резонансную частоту контура.

7. Вычислить относительную ошибку определения резонансной частоты контура.

ОФОРМЛЕНИЕ ОТЧЕТА

Отчет должен включать:

1.Название работы;

2.Фамилии и инициалы исполнителей, № группы;

3.Цель работы;

4.Рис.1 с пояснениями;

5.Уравнение (3) с пояснениями;

6.Расчетные формулы с пояснениями;

7.Таблицу 1;

8.Таблицу 2;

9.Графики резонансных кривых;

10.Результаты расчетов;

11.Выводы по работе;

12.Подписи исполнителей;

13.Дату выполнения работы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Поясните вывод уравнения вынужденных электромагнитных колебаний в элек­трическом контуре.

2.Охарактеризуйте поведение колебательного контура в момент резонанса.

3.Назовите параметры резонансной кривой контура.

ЛИТЕРАТУРА

1.Савельев И.В. Курс общей физики, т.2. Электричество и магнетизм. Учебное пособие для втузов. М.: Наука, 1978

2.Лабораторные занятия по физике: Учебное пособие для вузов / Л.Л.Гольдин и др..; Под ред. Л.Л.Гольдина. М.: Наука,1983.

3.Лабораторный практикум по физике: Учеб. пособие для студентов втузов / В.Ф.Алексеев и др.; Под ред. К.А.Барсукова и Ю.И.Уханова. М.: Высшая шко­ла, 1988.

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им.А.Н.Туполева

Кафедра прикладной физики

---

Дата добавления: 2015-08-02