Краткая теоретическая часть. Дифракцией света называют огибание лучами света контура непрозрачных тел

Дифракцией света называют огибание лучами света контура непрозрачных тел, соизмеримых с длиной волны излучения, и проникновение света в область геометрической тени.

Различают два случая дифракции света: дифракцию Френеля, или дифракцию в сходящихся лучах, и дифракцию Фраунгофера, или дифракцию в параллельных лучах.

ДИФРАКЦИЯ ФРАУНГОФЕРА

Дифракция на одной щели

Дифракцией Фраунгофера называют дифракцию в параллельных лучах. Чаще параллельность падающих на преграду лучей достигается установкой источника света в фокусе собирающей линзы. После преграды также ставится собирающая линза, в фокусе которой располагается экран.

Рассмотрим сначала свет, падающий перпендикулярно к плоскости щели (рис.1). Фронт волны совпадает с плоскостью щели. Поэтому все лучи находятся в фазе и в центре экрана возникает светлое пятно (нулевой максимум).

Рис.1.

Рассмотрим теперь (рис.2) лучи, идущие под углом θ₁ таким образом, что луч из верхнего края щели проходит на λ больший путь, чем луч из нижнего края щели. Луч из центра щели проходит путь на λ/2 больше, чем нижний луч. Эти лучи оказываются в противофазе и, интерферируя, гасят друг друга. Таким образом, каждый луч из нижней половины щели гасит соответствующий луч из верхней половины. Поэтому на экране под данным углом света не будет.

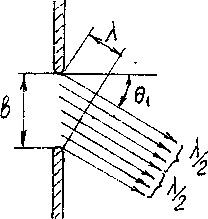
Рис.2.

Угол θ₁, при котором происходит гасящая интерференция, как видно из рис. 2, удовлетворяет соотношению λ = b · sin θ₁, откуда sin θ₁= 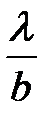- первый минимум света.

Интенсивность света максимальная при θ = 0 убывает до минимума при θ₁, задаваемым этим соотношением. Рассмотрим теперь (рис. 3) лучи. падающие под бòльшим углом θ₂, при котором разность хода верхнего и нижнего лучей составляет

В этом случае лучи из нижней трети щели, попарно интерферируя, гасят лучи из средней трети, т.к. в каждой паре лучи оказываются в противофазе. Свет верхней щели не гасится и доходит до экрана

Рис. 3

На экране под углом θ₂ возникает светлое пятно, но менее яркое, чем центральное пятно, соответствующее θ₀= 0. Из рис. 3. имеем

Sin θ₂ = 3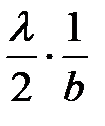

Это светлое пятно называется первым максимумом.

Рис. 4

Если увеличим угол наклона до θ₃ (рис.4) так, чтобы разность хода составила 2λ. Лучи из соседних зон находятся в противофазе и гасят друг друга. Поэтому на экране под углом θ₃ будет опять минимум интенсивности (второй минимум)

Sin θ₃ = 2 .

И так далее.

Окончательно получаем, что, если разность хода крайних лучей равна четному числу полуволн

b · sin θ = ± 2m , (1)

то на экране возникает минимум освещенности, при нечетном числе полуволн

b · sin θ = ± (2m +1) 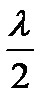, (2)

- максимум освещенности.

На экране получается (рис.5) следующее распределение интенсивности I света, т.е. дифракционная картина от щели.

Интенсивность максимумов значительно уменьшается с возрастанием их порядка. Так, расчеты показывают, что

I ₁ = 0,045 I ₀, I ₂ = 0,016 I ₀ и т.д., где I ₀ – нулевой, I ₁ - первый, I ₂ - второй максимумы интенсивности света I.

ДИФРАКЦИОННАЯ РЕШЕТКА

Дифракционная картина от одной щели или отверстия не имеет достаточной резкости и яркости, т.к. через узкую щель проходит мало света и светлые полосы получаются широкими и не яркими. Поэтому вместо одной щели берут несколько одинаковых щелей. С этой целью применяют так называемые дифракционные решетки.

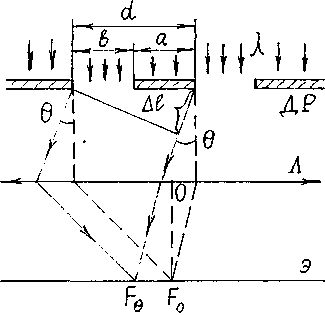
Рис. 6.

Простейшая одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. На рис.6 показаны только две щели решетки ДР. Ширину щели обозначим b, а ширину непрозрачных промежутков а. Величина d = а + b назы­вается периодом или постоянной дифракционной решетки.

Пусть на решетку падает плоская монохроматическая волна по нормали к поверхности. Все точки щелей находятся на одной волновой поверхности. Поэтому колебания в них происходят в одной фазе. Лучи, проходя через лин­зу Л, попадают на экран Э.

Лучи, не испытывающие в щелях отклонения, собираются на оптической оси линзы OF₀, и в результате усиливающей интерференции образуют светлое пятно (нулевой максимум).

Под углом θ, при котором лучи от соседних щелей обладают разностью хода ∆l = mλ (m - целое число), будет опять усиливающая интерференция, т.е будут наблюдаться максимумы. Следовательно, условие максимумов запишется в виде

d sin θ = ± mλ, (3)

где m = 0, 1, 2.... - порядок дифракционного максимума.

Таким образом, на экране наблюдаются светлые полосы, соответствующие различным значениям и симметрично расположенные относительно центральной полосы.

В случае дифракционной решетки максимумы интенсивностей I гораздо ярче и резче, чем в приборе с 1-й или 2-мя щелями, и пропорциональны числу щелей N. т.е.

I_max, ДР = N² I_{max IЩ}

где N - число щелей.

Дифракционные решетки часто изготавливают, нанося на стекло тонкие линии алмазным резцом. В настоящее время, например, для видимой и УФ-областей используют дифракционные решетки с числом штрихов от 300 до 1200 на 1мм.

Дифракционные решетки со щелями в непрозрачном экране называются прозрачными решетками. Кроме того, существуют отражательные решетки. Их изготавливают, нанося тонкие штрихи на металлическую или стеклянную поверхность. В этом случае дифракционную картину образует отраженный свет.

Дифракционная решетка служит важным элементом спектроскопа-прибора для точного измерения длин волн.

ПРАКТИЧЕСКАЯ ЧАСТЬ

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Схема лабораторной установки приведена на рис. 7.

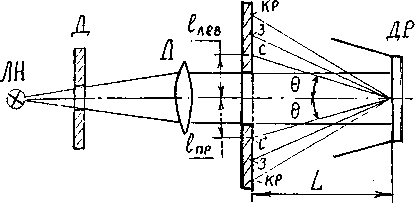
Рис. 7

Свет от лампы накаливания ЛН через диафрагму Д расширяющимся пучком падает на линзу Л. Далее свет параллельным пучком проходит через отверстие в экране Э и, отразившись от отражательной дифракционной решетки ДР, падает на непрозрачный экран Э. Справа и слева от центра на экране будут наблюдаться спектры первого (наиболее отчетливо) и второго порядков, обращенные к центру сине-фиолетовыми краями.

Полагая в формуле (3) sin θ = tg θ = , длину волны λ света можно вычислить как

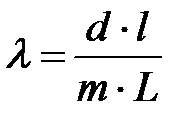, (4)

где для спектра первого порядка m = 1, второго – m = 2 и т.д. d = 1,8 мкм.

ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

1. После изучения теоретической части ознакомиться с лабораторной
установкой.

2. Включить установку в сеть с напряжением 12 В. Перемещая дифракционную решетку ДР с кожухом вдоль продольной оси, получить на экране Э четкое изображение правого и левого спектров первого порядка. Закрепить положение ДР винтом.

3. Линейкой измерить расстояние L (рис. 7) от экрана Э до дифракционной решетки ДР.

4. С помощью линейки со стрелкой измерить расстояния l _пр и l _лев для
полос синего, зеленого и красного цветов относительно центральной светлой
полосы. Результаты измерений занести в таблицу.

5. Ослабить винт фиксации положения ДР и чуть сместить её, расстроив
четкое изображение полос. Отключить установку.

6. Повторить действия по пунктам 2, 3,4, 5 ещё два раза.

Таблица

Цвет полосы спектра	l пр ,мм	l лев,мм	l ср, мм	λ^Э, мкм	δ, %
Красный
Зеленый
Синий

7. Вычислить средние значения и для всех цветов.

8. Для одного из цветов по методике прямых измерений записать полностью результаты измерений l _пр и l _лев.

9. Для каждого цвета вычислить и экспериментальные значения длин волн , , . Результаты занести в таблицу.

10. Полагая λ_кр = 0,7 мкм, λ₃ = 0,54 мкм. λ_с = 0,47 мкм, определить относительные ошибки измерений λ всех цветов по формуле

11. Сделать выводы по работе.

СОДЕРЖАНИЕ ОТЧЕТА

1. Краткая теория дифракции света и дифракционной решетки.

2. Схема лабораторной установки.

3. Таблица результатов измерений и вычислений.

4. Записи результатов измерений по методике прямых измерений.

5. Вычисления , , и δ_кр, δ_з, δ_с.

6. Выводы по работе.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение явления дифракции света.

2. Объясните появление спектров света при дифракции.

3. Объясните устройство, принцип действия и назначение дифракционной
решетки.

4. Поясните порядок расчетов длин волн цветовых спектров.

5. Объясните порядок полной записи результатов прямых измерений.

ЛИТЕРАТУРА

1. Трофимова Т.Н. Курс физики. М.: Высшая школа. 1999. 542 с.

2. Детлаф А.А., Яворский Б.М. Курс физики. М: Высшая школа. 2000. 718с.

Казанский государственный технический университет

им. А.Н. Туполева

Кафедра технической физики

Дата добавления: 2015-08-02